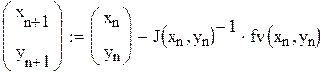Метод Ньютона для систем нелинейных уравнений
Пусть дана система
Согласно методу Ньютона последовательные приближения вычисляются по формулам
где а якобиан
Начальные приближения Метод Ньютона эффективен только при достаточной близости начального приближения к решению системы. Пример 4.1 Решить нелинейную систему уравнений в Mathcad с пятью верными знаками после запятой.
Преобразуем систему, выразив х из обоих уравнений.
Левые части уравнений исходной системы зададим в виде функций пользователя с двумя переменными.
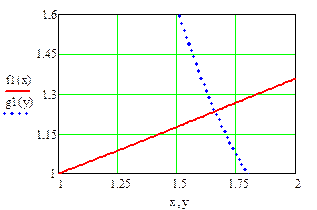
Правые части преобразованной системы зададим в виде функций пользователя от переменной y. Построим их на графике.
Ответ: x=1.23427 y=1.66153
Ответ: x=1.23427 y=1.66153 Рис.4.1. Решение примера 4.1 в Mathcad 4.2. Распространение метода Ньютона на системы из n уравнений с n неизвестными Рассмотрим нелинейную систему уравнений
с действительными левыми частями. Можно записать систему в более компактном виде:
где Для решения системы будем пользоваться методом последовательных приближений. Предположим, что найдено приближение на шаге p
где Введем в рассмотрение матрицу Якоби системы функций
Если эта матрица неособенная, т.е.
где Таким образом, последовательные приближения находятся по формуле:
За нулевое приближение
Пример 4.2 Решить систему из примера 4.1 в Mathcad в векторной форме.
Ответ: x=1.23427 y=1.66153
Рис.4.2. Решение примера 4.2 в Mathcad
|
,
,
, 
,
.
и 
определяются приближенно (графически и т.п.).
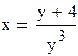
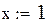
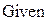
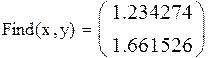
(4.1)
,
, а 
.
,
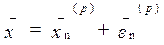- поправки (погрешность корня).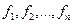
относительно переменных 
:
, то поправка 
выражается следующим образом:
,
- матрица, обратная матрице Якоби.
.
можно взять приближенное значение искомого корня.
