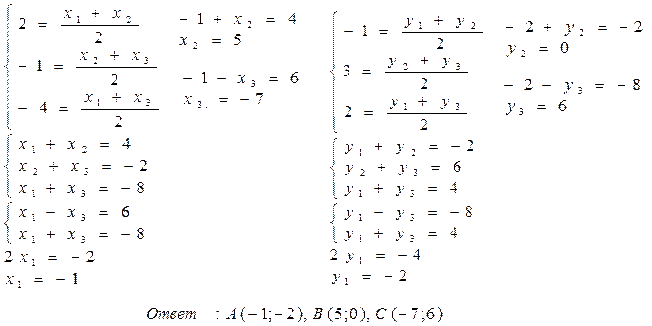Метод координат
В аналитической геометрии геометрические объекты – кривые и поверхности – изучаются при помощи алгебры. В основе такого изучения лежит метод координат, при котором положение точки на прямой плоскости или в пространстве определяется соответственно одним, двумя или тремя числами, координатами этой точки, а каждой кривой или поверхности соответствует одно или несколько уравнений, связывающих координаты всякой точки им принадлежащей.
 Подставим в уравнение. Подставим в уравнение.
½ =1/2*12(u) координаты точки M удовлетворяют уравнению y=(1/2)*x2
Определение. Ординатой точки называют расстояние этой точки до оси (OX). Ордината положительна, если точка расположена выше оси (OX), отрицательна, если точка ниже оси (OX).
Деление отрезка в заданном соотношении.
Выразим вектор
Из (2) подставим в (1)
Из
(5) поместим рисунок в систему координат так, чтобы точка О стала центром системы, тогда Равенство (5) является векторной формулой деления отрезка в данном отношении.
*
Формулы координат точки С, делящей отрезок АВ в отношении
Медианы в точке пересечения делятся в отношении
Задача 2. До какой точки надо продлить отрезок АВ(от А к В) чтобы длина его стала в четыре раза больше прежней.
Тогда по формулам **
|

 (3; 4)
(3; 4)
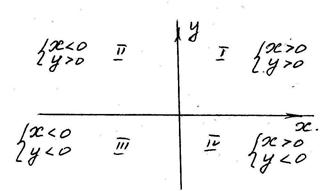 Определение. Абсциссой точки называют расстояние этой точки до оси (OY). Абсцисса положительна, если точка расположена справа от оси (OY), отрицательна, если точка слева от оси (OY).
Определение. Абсциссой точки называют расстояние этой точки до оси (OY). Абсцисса положительна, если точка расположена справа от оси (OY), отрицательна, если точка слева от оси (OY). Расстояние между двумя точками на плоскости.
Расстояние между двумя точками на плоскости.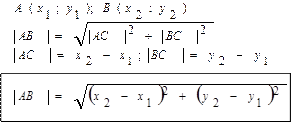
 Выберем точку О произвольно и зададим векторы:
Выберем точку О произвольно и зададим векторы: 
 через
через  и
и  .
.

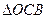 имеем
имеем 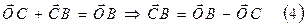
 из (4) – в (3)
из (4) – в (3)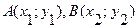 , координаты точки
, координаты точки  - неизвестны. Т.к. начало векторов ОА, ОВ, ОС – находятся в начале координат, то эти векторы называются радиус-векторами точек А, В, С (соответственно), тогда
- неизвестны. Т.к. начало векторов ОА, ОВ, ОС – находятся в начале координат, то эти векторы называются радиус-векторами точек А, В, С (соответственно), тогда 

 Чтобы получить координатные формулы необходимо подставить в (5) из (6) одноименные координаты.
Чтобы получить координатные формулы необходимо подставить в (5) из (6) одноименные координаты.
 (считая от А к В)Если отрезок АВ разделить точкой С на два равных отрезка, то
(считая от А к В)Если отрезок АВ разделить точкой С на два равных отрезка, то 



 Задача 1
Задача 1
 Найти центр тяжести треугольника. Центр тяжести треугольника находиться в точке пересечения медиан. Находим координаты точки М1 из условия:
Найти центр тяжести треугольника. Центр тяжести треугольника находиться в точке пересечения медиан. Находим координаты точки М1 из условия:


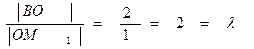 (от В к М1)
(от В к М1)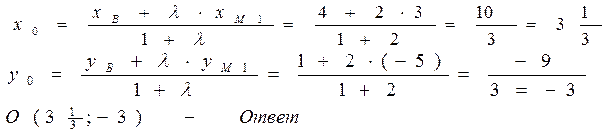

 Задача 3.
Задача 3. М1 (2; -1)М2 (-1; 3) М3 (-4; 2) есть координаты середины сторон треугольника. Найти координаты вершин треугольника.
М1 (2; -1)М2 (-1; 3) М3 (-4; 2) есть координаты середины сторон треугольника. Найти координаты вершин треугольника. Пусть
Пусть