ПАРАБОЛАПараболой называется множество точек плоскости расстояние от каждой из которых до точки, называемой фокусом и прямой, называемой директрисой, равны между собой. Расстояние от фокуса до директрисы |FK|=P и называется параметром параболы.
Парабола со смещенной вершиной. Пусть вершиной параболы будет точка А (х0; у0). |KF|=P, точка А делит |KF| напополам. у=у0 – ось симметрии F(x0+ Уравнение параболы (у-у0)2=2р(х-х0). Уравнения остальных парабол со смещенной вершиной будут выглядеть так: (у-у0)2=-2р(х-х0) – ось симметрии || (ОХ), ветви направлены влево. (x-x0)2=
Пример №1.
у2-8у-8х-8=0 у2-8у=8х+8 у2-2·4·у+42=8х+8+42 (у-4)2=8х+24 (у-4)2=8(х+3)
у=4 – ось симметрии ветви параболы вправо.
|
N(- 
; y). NM {x+ 
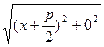; |FM| = 
= 
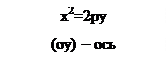
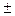2р(y-y0) – ось симметрии || (ОУ), ветви направлены вверх, если (+), вниз, если (-).
А (-3; 4) 2p=8 
F(-3+2; 4)=(-1; 4), x=-3-2=-5. x=-5 – директриса,
