Угол между прямыми
l 1 : A1x+B1y+C1=0, l 2 : A2x+B2y+C2=0,
Найдем cos φ = где | Если l 1 || l 2, то φ =0 или φ =π Þ cos φ = Если l 1 Если φ < 900, то Þ cos φ > 0 Если 900< φ < 1800, то Þ cos φ < 0 |cos φ |
α 2= α 1+ φ Þ φ = α 2- α 1 tg φ =tg(α 2- α 1) = tg α 2=k2, tg α 1=k1. Тогда tg φ = Формула tg φ, φ образован при повороте прямой l 1 вокруг точки В до совмещения с прямой l 2 (против часовой стрелки). Если l 1|| l 2, то φ =0 и φ =1800Þ k2=k1 Если l 1 т.е. Если l 1 Если 900< φ < 1800, то tg φ < 0.
l 1 имеет k1 и l 2 имеет k2 и l 1 : A1x+B1y+C1=0 l 2 : A2x+B2y+C2=0 Если l 1
 A1x+B1y+C1=0
A2x+B2y+C2=0 * Если l 1|| l 2, то ** Если l 1 Если l 1= l 2, то * и ** есть условия параллельности и перпендикулярности прямых.
Найдем координаты векторов, которые
AC {x3-x1; y3-y1} По определению векторного произведения векторов (лекция 3 п.1).
 так как  =1, то
SABCD =
SABC=
Пример: А (2; -3) В(4; 2) С(-1; 5)
   а) АВ {2; 5} AC {-3; 8}
SABC =
|
Определение. За угол между прямыми принимаются наименьший из углов образованных этими прямыми.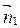
{A1; B1}.
{A2; B2}.
l1l2 = 
; | 
;
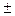1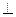
l 2, то φ =900 и Þ cos φ =0
1.!
Угол α 2 – внешний угол треугольника АВС
.
= 0 Þ 1+k2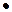 
k1=0, k2=-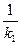 
l2 =B, φ < 900, то tg φ > 0.
В) Взаимное расположение двух прямых.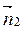
Þ 
= 
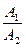и k1=k2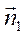
Þ A1 •A2+B1 •B2=0 и k2=- 
= 
= 
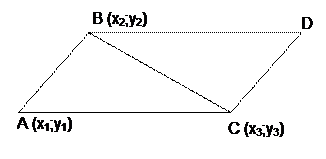13) Площадь параллелограмма и треугольника.
образуют данный параллелограмм.
АВ {x2-x1; y2-y1}
SABCD=|AB•AC|
SABC= 
-31| = 
