Уравнение прямой в общем виде
а) Пусть А=С=0, В Ву=0, следовательно у=0 – ось (ОХ) б) Пусть В=С=0, А Ах=0, следовательно х=0 – ось (ОУ) в) Пусть А=В=0, С 0=С (такого быть не может) г) Пусть А=0, В Ву+С=0, следовательно у=- д) Пусть В=0, А Ах+С=0, следовательно х=-
Ах + Ву = 0 Þ у=
ж) Пусть А¹ 0, В¹ 0, С¹ 0. Ах+Ву = -С Þ у = у = κ х + в, - прямая не проходит через начало координат. Получим, что уравнение Ах+Ву + С = 0 при различных значениях А, В, С содержит в себе все случаи взаимного расположения прямой осей координат. Значит уравнение Ах+Ву + С = 0 - уравнение прямой в общем виде. 2) Уравнение прямой в отрезках.
-
Если х=0Þ у= b; В(0; b). У=0Þ х= а; А(a; 0)
|
Докажем, что уравнение Ах+Ву+С=0 – уравнение первой степени с двумя неизвестными является уравнением прямой при различных значениях А, В, С.
0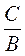
= в, у=в || (OX)
=а, х=а || (ОУ).
е) Пусть С=0, А¹ 0, В¹ 0.
Þ у = 
• x 
)
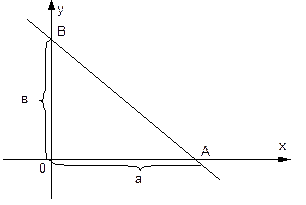Преобразуем Ax+By+C=0
Ax+By=-C: (-C)
•x+ (- 
)•y=1
