Каноническое и параметрическое уравнение прямой
  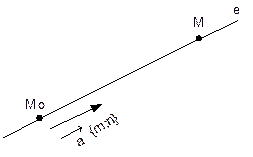 Пусть Пусть 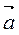 {m, n} и {m, n} и 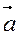 // l. // l.  - направляющий вектор прямой. М0 (х0; у0), М(х; у). М0М {x-x0 ; y-y0}, так как - направляющий вектор прямой. М0 (х0; у0), М(х; у). М0М {x-x0 ; y-y0}, так как 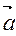 // М0МÞ t // М0МÞ t  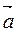 , где t , где t  R (R – множество R (R – множество
действительных чисел)
параметрическое уравнение прямой каноническое уравнение прямой 8) Расстояние от точки до прямой
M0 (x0; y0)
Ах1+Ву1+С=0 (и) Þ С=-Ах1-Ву1
в) Найдем
Из подставим во и получим
Сравним и.
L1: A1x+B1y+C1=0 L2: A2x+B2y+C2=0
тогда | MM1 | = | MM2 | - есть векторы уравнения биссектрисы D1=D2 (Расстояния от точки М (х; у) до прямых L1 и L2 одинаковы).
Пример №1. Написать уравнение биссектрисы угла, образованного прямыми L1, L2, в котороым лежит точка О (0; 0). L1: x1+2y-5=0; L2: 3x-6y+2=0; тогда
Проверим знак прямых L1 и L2 в точке О (0; 0). L1: 0+2
 |x+2y-5|=-(x+2y-5) |x+2y-5|=-(x+2y-5)
|3x-6y+2|=3x-6y+2 - -3x-6y+15=3x-6y+2 Þ 6x-13=0 Уравнение биссектрисы. x=
|


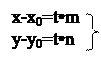


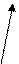
 а) L: Ах+Ву+С=0
а) L: Ах+Ву+С=0 {A, B};
{A, B}; M1(x1; y1)
M1(x1; y1)  б) l имеет
б) l имеет 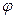 =00 или
=00 или 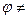 1800
1800
 (
( - угол между
- угол между 
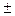 1. M1M0 {x0-x1; y0-y1}.
1. M1M0 {x0-x1; y0-y1}.





 г)
г) 

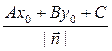 Þ
Þ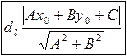
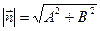

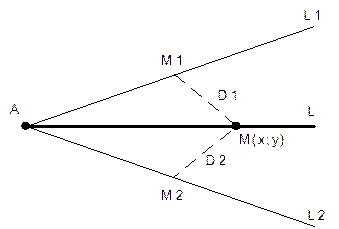 9) Уравнение биссектрисы угла.
9) Уравнение биссектрисы угла.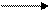
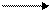 L – биссектриса угла А. М(х; у)
L – биссектриса угла А. М(х; у)  =
= 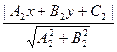
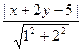 =
= 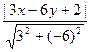 Þ
Þ  =
= 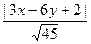
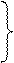 L2: 0-0+2=2; > 0, при этих условиях раскрываем модули:
L2: 0-0+2=2; > 0, при этих условиях раскрываем модули:
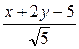 =
= 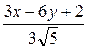
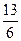 Þ, биссектриса параллельна ОУ.
Þ, биссектриса параллельна ОУ.


