Матричная запись системы линейных уравнений
a2x+в2у+с2z=d2 а3x+в3у+с3z=d3 Введем обозначения:
А = a2 в2 с2 ; Χ = у Д= d2 а3 в3 с3 z d3 Тогда система запишется следующим образом X-неизвестный вектор - столбец. Д-известный вектор - столбец. А∙ Х=Д Определение: обратной для матрицы «А» называется такая матрица, которая удовлетворяет условию. А-1∙ А=A∙ A-1=E, где Е – единичная матрица.
А1/∆ A2/∆ A3/∆ А-1= B1/∆ B2/∆ B3/∆, где Ai; Bi; Ci –алгебраические дополнения соответственно C1/∆ C2/∆ C3/∆ элементов ai вi ci (i=1, 2, 3). Тогда решение системы будет: А∙ Х=Д | ∙ А-1 Пример. Решить систему по формулам Крамера и матричным способом. А) Метод Крамера:
2x+y+z=-1 ∆ = 2 1 1 = 1+6+2-1-4-3=9-8=1 x+3y+z=2 1 3 1 имеет единственное решение.
∆ x= -1 1 1 = 1+4-2-2+2-3=7-8=-1 2 3 1
∆ y= 2 -1 1 = -1+4+1+1-2-2=6-5=1 1 2 1
∆ z= 2 1 -1 = 2+6-2-2-8+3=-11+11=0 1 3 2
x= Ответ: (-1; 1; 0) Б) Матричным способом. ∆ =1 (найдено в А) ai bi ci
Составим матрицу А= 2 1 1; Д= -1 1 3 1 2 Находим алгебраические дополнения А1 =
B1 = (-1)1+2
C1 = (-1)1+3
-2/1 1/1 1/1 -2 1 1 A-1= -1/1 0/1 1/1 = -1 0 1 5/1 -1/1 -3/1 5 -1 -3
Ответ: (-1; 1; 0)
В) Метод последовательного исключения неизвестных (метод Гаусса, немецкий математик, 1777-1855 гг.) Рассмотрим эту же систему:
2x+y+z=-1 x+3y+z=2
1 2 1 1 2 1 1 -1 ~ 1 3 1 2
1 2 1 1 1 2 1 1 1 2 1 1 0 -3 -1 -3 ~ 0 1 0 1 ~ 0 1 0 1 0 1 0 1 0 -3 -1 -3 0 0 -1 0
x+2y+z=1 y=1 -z=0 Ответ: (-1; 1; 0).
|

 а1x+в1у+с1z=d1
а1x+в1у+с1z=d1

 a1 в1 c1 х d1
a1 в1 c1 х d1 Если
Если  , то
, то A∙ A-1∙ X=Д ∙ А-1
A∙ A-1∙ X=Д ∙ А-1 

 x+2y+z=1 1 2 1
x+2y+z=1 1 2 1 0
0 1 2 1
1 2 1
 1 1 1
1 1 1
 1 2 1
1 2 1 =
=  =-1; y=
=-1; y=  =1; z=
=1; z=  =0
=0
 1 2 1 1
1 2 1 1 ∙ (-1)1+1=1-3=-2; A2 = (-1)2+1∙
∙ (-1)1+1=1-3=-2; A2 = (-1)2+1∙  = -1∙ (2-3)=1; A3 = (-1)3+1∙
= -1∙ (2-3)=1; A3 = (-1)3+1∙  = 2-1=1
= 2-1=1 = -1; B2 = (-1)2+2 ∙
= -1; B2 = (-1)2+2 ∙ 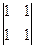 = 0; B3 = (-1)3+2
= 0; B3 = (-1)3+2  = -1(-1)=1
= -1(-1)=1 = 6-1=5 C2 = (-1)2+3
= 6-1=5 C2 = (-1)2+3  = -1 C3 = (-1)3+3
= -1 C3 = (-1)3+3  = 1-4=-3.
= 1-4=-3.



 x+2y+z=1
x+2y+z=1
 Составим для этой системы расширенную матрицу.
Составим для этой системы расширенную матрицу.



 Обнулим во второй строке первый элемент, в третьей строке первый и второй элементы.
Обнулим во второй строке первый элемент, в третьей строке первый и второй элементы. Запишем систему, соответствующую конечной матрице:
Запишем систему, соответствующую конечной матрице:


