ГИПЕРБОЛА
||F1M|-|FM||= 2a, 2a< 2c |FF1|= 2c - Векторное уравнение гиперболы. Аналогично выводу уравнения эллипса. При условии, что в2= с2-а2.
|AA1|=2 a – вещественная ось гиперболы. B; B1 (0; |BB1|=2 в – мнимая ось гиперболы. F; F1( |FF1|=2c – фокусное расстояние. (МР) и (NQ) - асимптоты гиперболы. У= Эксцентриситетом гиперболы называется отношение фокусного расстояния и длина вещественной оси гиперболы. е = Если е Если е
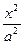 + + 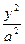 =1, где а2=с2-а2, =1, где а2=с2-а2,
x2-y2=a2 (уравнение равносторонней гиперболы), где с2=2а2 e = e= (MN); (NQ): y=
|



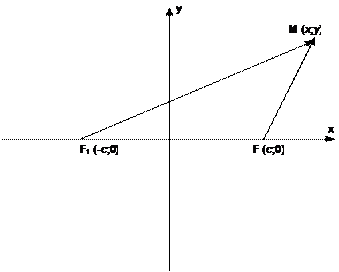 Гиперболой называется множество точек плоскости, модуль разности расстояний от каждой из которых, до двух точек плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.
Гиперболой называется множество точек плоскости, модуль разности расстояний от каждой из которых, до двух точек плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами. =1, где в2= с2-а2.
=1, где в2= с2-а2.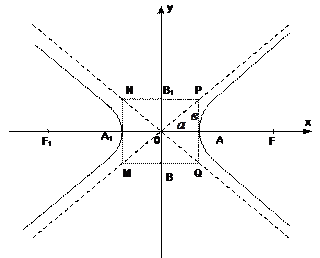 A; A1(
A; A1(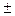 a; 0) – вещественные вершины гиперболы.
a; 0) – вещественные вершины гиперболы.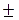 в) – мнимые вершины гиперболы.
в) – мнимые вершины гиперболы.
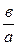 ·х – уравнение асимптот гиперболы.
·х – уравнение асимптот гиперболы. =
= 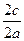
 е =
е = 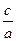 , так как a< c, тоe > 1.
, так как a< c, тоe > 1.
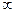 , то с
, то с 
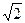
 =
= 


