 К кривым второго порядка относятся эллипс, окружность, гипербола, парабола. Кроме того, в некоторых случаях уравнение второй степени может определить две прямые, точку и мнимое геометрическое место. Все эти линии являются частными случаями уравнения второй степени с двумя неизвестными.
К кривым второго порядка относятся эллипс, окружность, гипербола, парабола. Кроме того, в некоторых случаях уравнение второй степени может определить две прямые, точку и мнимое геометрическое место. Все эти линии являются частными случаями уравнения второй степени с двумя неизвестными.
Ах2+Ву2+Сху+Dх+Еу+F=0 (*)
Окружность.
Окружностью называется множество точек плоскости расстояние от каждой из которых до точки, называемой центром, есть величина постоянная, называемая радиусом окружности.
 Пусть точка О1(х0; y0), М(х; у) – принадлежит окружности, тогда по определению |O1M|=r – это есть векторное уравнение окружности.
Пусть точка О1(х0; y0), М(х; у) – принадлежит окружности, тогда по определению |O1M|=r – это есть векторное уравнение окружности.

 O1M {x-x0; y-y0} |O1M| =
O1M {x-x0; y-y0} |O1M| =  = r.
= r.
(x-x0)2+(y-y0)2=r2
 Если М1 (0; у0), то окружность с центром в этой точке имеет уравнение:
Если М1 (0; у0), то окружность с центром в этой точке имеет уравнение:
х2+(y-y0)2=r2 – (ω 1).
Если М2(х0; 0), то (х-х0)2+у2=r2 - (ω 2)
Если О (0; 0), то х2+у2=r2 – (ω 3).
Покажем, что при условии А=В и С=0 уравнение * есть уравнение окружности.
Ах2+Ау2+Dх+Еу+F=0 |: A
x2+y2+  x+
x+  y+
y+  =0
=0
(x2+2 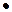

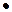 x+
x+  )+(y2+2
)+(y2+2 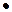

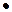 y+
y+ 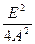 ) = -
) = -  +
+  +
+ 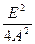
(x+  )2+(y+
)2+(y+  )2 = (
)2 = ( )2 – это есть окружность с центром в точке
)2 – это есть окружность с центром в точке
М0 (-  ; -
; -  ) и r=
) и r=  .
.
 ЭЛЛИПС.
ЭЛЛИПС.

 Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых, до двух точек, называемых фокусами, есть величина постоянная большая, чем расстояние между фокусами.
Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых, до двух точек, называемых фокусами, есть величина постоянная большая, чем расстояние между фокусами.
|F1M| + |FM|= 2a – векторное уравнение.
2a> 2c
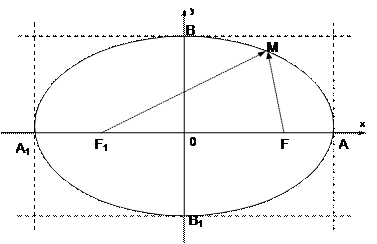

 |FF1|= 2c, следовательно F1(-c; 0), F(c; 0), M(x; y).
|FF1|= 2c, следовательно F1(-c; 0), F(c; 0), M(x; y).
|F1M| = 
|FM| = 
 +
+  = 2a
= 2a
Избавимся от иррациональности и введем величину в2=а2-с2.
Тогда получим уравнение 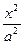 +
+  =1, где в2=а2-с2.
=1, где в2=а2-с2.
А1; А – вершины эллипса А1 ; А(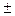 а; 0)
а; 0)
В1 ; В - вершины эллипса В1 ; В (0; 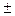 в).
в).
F1 ; F – фокусы эллипса F1 ; F(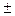 c; 0)
c; 0)
|А1A|=2 a – большая ось эллипса.
|BB1|=2 в – малая ось эллипса.
 |FF1|=2 c – фокусное расстояние эллипса.
|FF1|=2 c – фокусное расстояние эллипса.
| фокальные радиусы точки М. r1+r=2a
| |


|F
1M|=r
1
|FM|=r
Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси его.
 e=
e=  =
= 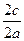 =
= 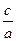
 e=
e= 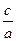 , так как а> c, то 0
, так как а> c, то 0  e
e  1.
1.
Если е  1, то с
1, то с  а, следовательно в
а, следовательно в  0 – эллипс сужается к оси(ОХ).
0 – эллипс сужается к оси(ОХ).
Если е  0, то с
0, то с  0, следовательно в
0, следовательно в  а – эллипс стремится занять положение окружности.
а – эллипс стремится занять положение окружности.
Если е=0, то с =0, следовательно в=а, 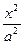 +
+  =1, где а2=а2-с2.
=1, где а2=а2-с2.
х2+у2=а2 и с=0, следовательно F1=F=0 – центр окружности.
Окружность – есть честный вид эллипса при условии, что, а=в.
 Если фокусы находятся на оси (ОУ), то уравнение
Если фокусы находятся на оси (ОУ), то уравнение 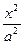 +
+  =1, где а2=в2-с2.
=1, где а2=в2-с2.
е=  =
= 
 e=
e=  .
.
A1(-  ; 0) ; 0)
| |
Если центр эллипса смещен в т. М
0(х
0; у
0),
то уравнение эллипса будут:
 +
+  =1, в2=a2-с2, - на (ОХ).
=1, в2=a2-с2, - на (ОХ).
 +
+  =1, а2= в2-с2, - на (ОУ).
=1, а2= в2-с2, - на (ОУ).
Пример №1.
 +
+  =1. Найти все элементы эллипса.
=1. Найти все элементы эллипса.
a2=64, в2=36, в2=а2-с2  с2=а2-в2=64-36=28
с2=а2-в2=64-36=28
а=8; в=6; с=2 
 А; А1 (
А; А1 (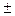 8; 0); B; B1 (0;
8; 0); B; B1 (0; 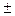 6); F; F1(
6); F; F1(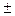 2
2  ; 0).
; 0).
|AA
1|=2a=16; |BB
1|=2в=12; |FF
1|=2c=4

e =  =
=  =
=  =
= 
Пример №2.
Составить уравнение эллипса, если большая ось равна 50, фокусы находятся на оси (ОУ) и е = 0, 6.
Так как F1F находятся на оси (ОУ), то:
 +
+  =1, где а2=в2-с2, e=
=1, где а2=в2-с2, e=  .
.
|BB1| - большая ось эллипса  2 в =50
2 в =50  в =25.
в =25.
 =0, 6
=0, 6  с =0, 6· 25
с =0, 6· 25  с =15; a 2=252-152=500.
с =15; a 2=252-152=500.
Получим  +
+  =1 – ответ.
=1 – ответ.

 |F1M|=r1
|F1M|=r1


 К кривым второго порядка относятся эллипс, окружность, гипербола, парабола. Кроме того, в некоторых случаях уравнение второй степени может определить две прямые, точку и мнимое геометрическое место. Все эти линии являются частными случаями уравнения второй степени с двумя неизвестными.
К кривым второго порядка относятся эллипс, окружность, гипербола, парабола. Кроме того, в некоторых случаях уравнение второй степени может определить две прямые, точку и мнимое геометрическое место. Все эти линии являются частными случаями уравнения второй степени с двумя неизвестными. Пусть точка О1(х0; y0), М(х; у) – принадлежит окружности, тогда по определению |O1M|=r – это есть векторное уравнение окружности.
Пусть точка О1(х0; y0), М(х; у) – принадлежит окружности, тогда по определению |O1M|=r – это есть векторное уравнение окружности.
 O1M {x-x0; y-y0} |O1M| =
O1M {x-x0; y-y0} |O1M| =  = r.
= r. Если М1 (0; у0), то окружность с центром в этой точке имеет уравнение:
Если М1 (0; у0), то окружность с центром в этой точке имеет уравнение: x+
x+  y+
y+  =0
=0

 )+(y2+2
)+(y2+2 
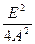 ) = -
) = -  )2 – это есть окружность с центром в точке
)2 – это есть окружность с центром в точке .
. ЭЛЛИПС.
ЭЛЛИПС. Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых, до двух точек, называемых фокусами, есть величина постоянная большая, чем расстояние между фокусами.
Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых, до двух точек, называемых фокусами, есть величина постоянная большая, чем расстояние между фокусами.



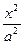 +
+  =1, где в2=а2-с2.
=1, где в2=а2-с2.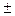 а; 0)
а; 0) e=
e=  =
= 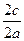 =
= 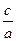
 e=
e=  e
e  1, то с
1, то с  Если фокусы находятся на оси (ОУ), то уравнение
Если фокусы находятся на оси (ОУ), то уравнение  =
= 
 e=
e=  .
. ; 0)
; 0)
 +
+  =1, в2=a2-с2, - на (ОХ).
=1, в2=a2-с2, - на (ОХ). +
+  =1. Найти все элементы эллипса.
=1. Найти все элементы эллипса. с2=а2-в2=64-36=28
с2=а2-в2=64-36=28
 А; А1 (
А; А1 ( ; 0).
; 0). =
=  =
=  =
= 
 +
+  =1, где а2=в2-с2, e=
=1, где а2=в2-с2, e=  .
. 2 в =50
2 в =50  =0, 6
=0, 6  с =15; a 2=252-152=500.
с =15; a 2=252-152=500. +
+  =1 – ответ.
=1 – ответ.


