В равенстве (1) перейдем к пределу при х 0
Это есть геометрический смысл производной функции.
(M0K) – касательная. (M0N) (M0N) – нормаль к графику. y-y0=k Если k=kкасат.=f/(x0), то у-у0=f/(x0) Если k=kнорм.=
Правила дифференцирования функции. Для нахождения производной можно воспользоваться алгоритмом, но эта работа будет очень трудоемкой и нерациональной. Этим алгоритмом можно воспользоваться для вывода формул дифференцирования подразделив все функции на большие классы. А затем использовать эти формулы для различных функций в этих классах. Основные формулы дифференцирования: 1. (с/)=0 (с-const). 2. (x)/=1. 3. (u+v-w)/=u/+v/-w/, где u, v, w – есть функции от х. 4. (u 5. (u 6. 7. (ln u)/ = 8. (аu)/ = аu 9. (um)/ = m 10. (sin u)/ = cos u 11. (cos u)/ =-sin u 12. (tg u)/ = 13. (ctg u)/ = - 14. (arcsin u)/ = 15. (arccos u)/ = - 16. (arctg u)/ = 17. (arcctg u)/ = - 18. y=f(ц(x)), то y/=f/ц 19. x=f(t) и у=ц(t), то y/x = 20. Дифференцирование неявной функции. а) Продифференцировать функцию по х, учитывая, что у=f(x). б) Разрешить полученное выражение относительно у/.
|

 Lim
Lim  х
х  0, tg
0, tg 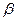 =lim
=lim 
 tgd=y/(x0), но tgd=Kкасат., значит у/(х0) – есть угловой коэффициент касательной, проведенной к данной кривой у=f(x) в данной точке х0.
tgd=y/(x0), но tgd=Kкасат., значит у/(х0) – есть угловой коэффициент касательной, проведенной к данной кривой у=f(x) в данной точке х0.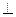 (M0K).
(M0K). (x-x0) – уравнение прямой с угловым коэффициентом.
(x-x0) – уравнение прямой с угловым коэффициентом. =
=  , то у-у0=
, то у-у0=  .
. , (logau)/ =
, (logau)/ =  .
. )/ =
)/ =  .
. .
. .
. .
. .
. , - функция задана параметрически.
, - функция задана параметрически.


