Исследования функции с помощью второй производной
Функция у=f(x) называется выпуклой в точке М1, если все точки, близкие к точке М1, находятся ниже касательной, проведенной в точке М1. Если функция выпукла в каждой точке (а; в), то говорят, что функция выпукла в (а; в) Существует достаточный признак выпуклости графика функции: y=f(x)
Функция у=f(x) называется вогнутой, точке М2, если все точки, близкие к точке М2, находятся выше касательной, проведенной в точке М2. Аналогично определение вогнутости на (а; в) Существует достаточный признак вогнутости графика функции. y=f(x) Отсюда возникает необходимый признак точки перегиба (точка, отделяющая выпуклую и вогнутую части графика). В точке М1 и М2 1) y//(x1)=y//(x2)=0 2) y//(x1-б)< 0 а y//(x1+б)> 0. 3) y//(x2-б)> 0 а y//(x2+б)< 0, (то есть при переходе через точки х1 и х2, знак у// меняется). Смена знака у// производной может происходить и в точках, в которых у// не существует. y=f(x), y/(x1) – не существует, значит и у//(х1) – не существует, но y//(x1-б)< 0 а y//(x1+б)> 0.
|


 не [a; в], если у//< 0 во всех х
не [a; в], если у//< 0 во всех х  [a; в].
[a; в].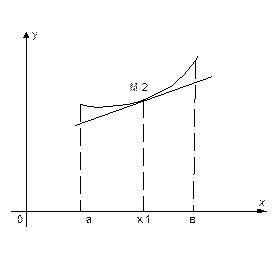
 на [a; в), если y//> 0 во
на [a; в), если y//> 0 во  х
х 


