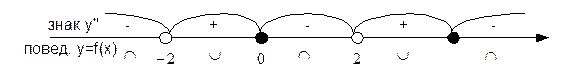Асимптоты графика функции
Определение: Асимптотой графика функции у=f(x) называется прямая линия, к которой неограниченно приближается уходящая в бесконечность ветвь графика (хотя бы пересекая эту прямую бесчисленное множество раз). Уравнение асимптоты. у=kx+в, если она наклонная, у=в, если она параллельна оси ОХ, х=а, если она параллельна оси ОУ.
Если k=0, то в= Если Исследовать функцию и построить ее график. у= 1. О.О. x2-4 2. y 3. Четность можно определить, так как область определения функции симметрична относительно нуля. f(-x)= Следовательно, график функции симметричен относительно начала координат. 4. Корни 5. Промежутки законопостоянства функции.
6. Исследуем с помощью предела Асимптоты: lim lim Отыскиваем наклонную асимптоту в виде у=kx+в. k=lim = 7. Исследуем с помощью первой производной:
у/=0 у/ - не существует. x1, 2=0, x3, 4= (в точках +2, -2, и х=0 не происходит смены знака у/, так как х2 и (х2-4)2 – всегда положительны). ymax=f(-2 8. Исследуем с помощью второй производной. у//= ( = 8.3 уперегиб.=f(0)=0. В точке х=+2 и х=-2 – перегиба нет, так как в этих точках у=f(x) не существует. 9. Строим график функции по проведенному исследованию.
|

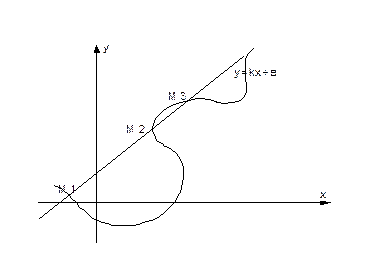 Пусть нам дана функция f(x), тогда для определений k – углового коэффициента
Пусть нам дана функция f(x), тогда для определений k – углового коэффициента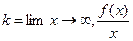 , а для
, а для 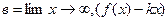
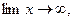 f(x), если в – существует, то у=в – горизонтальная асимптота.
f(x), если в – существует, то у=в – горизонтальная асимптота.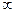 , то х=а – вертикальная асимптота.
, то х=а – вертикальная асимптота.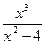
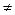 0
0  x
x 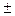 2
2 ]
] 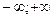 [ - множество значений функции.
[ - множество значений функции.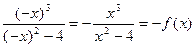 - функция нечетная.
- функция нечетная.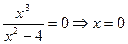
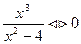
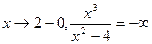 ; lim
; lim 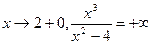
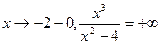 ; lim
; lim 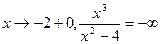 , x-2 – вертикальная асимптота.
, x-2 – вертикальная асимптота.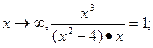 в=lim
в=lim 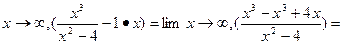
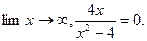 y=1
y=1 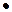 x+0; y=x – наклонная асимптота.
x+0; y=x – наклонная асимптота. у/=
у/= 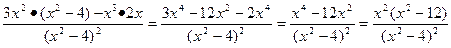 .
.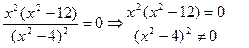
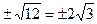 , x5, 6=
, x5, 6= 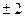 - точки разрыва функции и в этих точках функция недифференцируема.
- точки разрыва функции и в этих точках функция недифференцируема.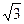 )=
)= 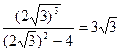 , yперегиб «колено»=f(0)=
, yперегиб «колено»=f(0)= 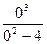
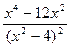 )/ =
)/ =  =
= 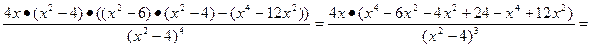
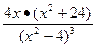 .
.