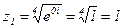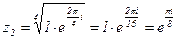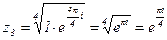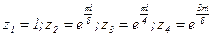Возведение в натуральную степень
Пример 8.
По определению корня имеем:
Из условия равенства двух комплексных чисел (см. пример 3) имеем:
Используя теорему Виета, получаем:
т. к. - если х=2, то у=-1, Þ - если х=-2, то у=1Þ Ответ:
Пример 9.
Можно сделать вывод, если a=0, то z=вi – чисто мнимые числа расположены на оси (OY) – которую иногда называют мнимой осью, а все действительные числа (если в=0), находятся на оси (OX) – её называют действительной осью. Выполнение действий над комплексными числами в геометрической форме ограничены: сложение, вычитание, умножение на число и скалярное и векторное произведение. Эти действия выполняются как действия над векторами, которые мы рассматривали в теме векторы. Геометрическая форма нам необходима для перехода от алгебраической формы и тригонометрической. 3.3. Тригонометрическая форма
φ – аргумент комплексного числа, r - модуль комплексного числа
Пусть нам дано комплексное число
Пример 11.
В тригонометрической форме легче выполнить действия умножение, деление, возведение степень и извлечение корня. Для этого используются формулы:
При умножении
При делении
При возведении в степень:
При извлечении корня n-ой степени: Пример 12.
Преобразуем число -1 в комплексную форму:
j=p -1=1× (cosp+i sinp)
если k=0, то если k=1, то если k=2, то если k=3, то если k=4, то Примечание:
Пример 13. Найти все корни уравнения х3-8=0. Уравнение nй степени имеет ровно n корней, значит это уравнение имеет три корня. х3=8 8=8+0i; а=8; в=0;
если k=0, то х1=2× (cos0+i sin0)=2(1+i× 0)=2+0i если k=1, то если k=2, то Ответ: х1=2; х2, 3=-1±i 3.4. Показательная форма По известному замечательному пределу Существует доказательство формулы: еz=еа+вi=ea× (cos в+sin в), если а=0, то формула принимает вид: еz=евi=e0(cos в+isin в)=, т.е. евi=cos в+isin в - формула Эйлера. По формуле Эйлера при условии в=j имеем: cosj+isinj=eij. Умножим обе части на r× (cosj+i sinj)=r× eij -есть формула перехода от тригонометрической формулы в показательную. Пример 14 (продолжение примера 10).
Пример 15 (продолжение примера 11).
Действия над комплексными числами в показательной формуле. Умножение: Деление: Возведение в степень: Извлечение корня: Пример 16.
если k=0, то если k=1, то если k=2, то если k=3, то Ответ:
|

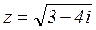 - результатом извлечения корня будет тоже комплексное число, т.е.
- результатом извлечения корня будет тоже комплексное число, т.е.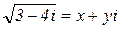 Наша задача найти x и y.
Наша задача найти x и y.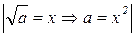
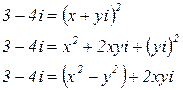
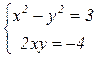 Û Решаем полученную систему:
Û Решаем полученную систему: 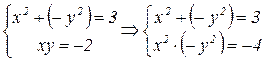
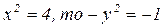
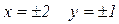
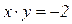 , то выбираем значения х и у с разными знаками, т. е.
, то выбираем значения х и у с разными знаками, т. е.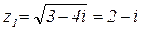
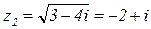
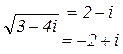
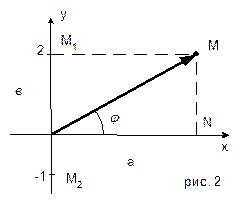 3.2. Геометрическая форма
3.2. Геометрическая форма
 z=a+вi – этому числу соответствует упорядоченная пара чисел (а; в), а значит точка М (а; в) или вектор ОМ (а; в).
z=a+вi – этому числу соответствует упорядоченная пара чисел (а; в), а значит точка М (а; в) или вектор ОМ (а; в). Геометрически комплексные числа, есть точка координатной плоскости или радиус-вектор т. М (а; в), где «а»- действительная часть комплексного числа, а «в» - коэффициент мнимой части комплексного числа.
Геометрически комплексные числа, есть точка координатной плоскости или радиус-вектор т. М (а; в), где «а»- действительная часть комплексного числа, а «в» - коэффициент мнимой части комплексного числа.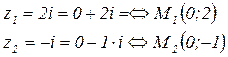
 Рассмотрим на рис. 2 треугольник ONM – прямоугольный. Величина угла MON равна φ (фи),
Рассмотрим на рис. 2 треугольник ONM – прямоугольный. Величина угла MON равна φ (фи), 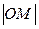 = r =
= r = 


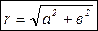 Формулы, выражающие зависимость между a; в и r; φ;.
Формулы, выражающие зависимость между a; в и r; φ;.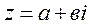 , умножим и разделим это число на r(r> 0) от этого значение комплексного числа не изменится.
, умножим и разделим это число на r(r> 0) от этого значение комплексного числа не изменится.

 получим тригонометрическую форму комплексного числа, где
получим тригонометрическую форму комплексного числа, где 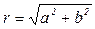 ,
, 
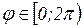 вычисляется по формулам
вычисляется по формулам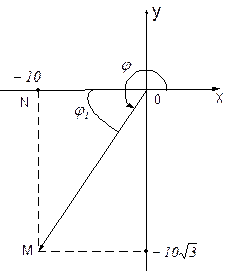 Пример 10. Получить тригонометрическую форму комплексного числа
Пример 10. Получить тригонометрическую форму комплексного числа  Изображаем графически это число
Изображаем графически это число
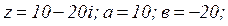
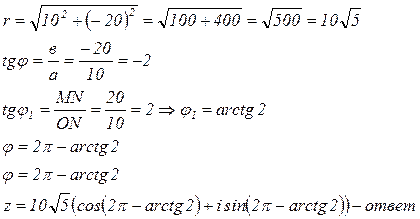

 :
: 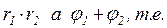
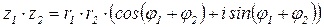
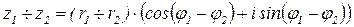
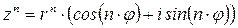 формула Муавра (А. Муавр (1667-1754) англ. математик)
формула Муавра (А. Муавр (1667-1754) англ. математик)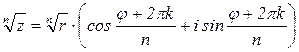 , где k=0; 1; 2; …n-1
, где k=0; 1; 2; …n-1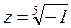
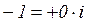 ;
; 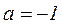 ; в=0
; в=0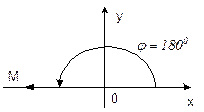
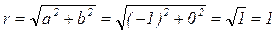
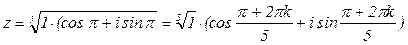 , где k=0, 1, 2, 3, 4
, где k=0, 1, 2, 3, 4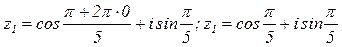
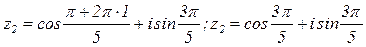
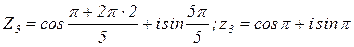
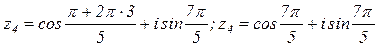

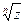 имеет ровно n значений, которые получаются при значениях k=0; 1; 2; …n-1.
имеет ровно n значений, которые получаются при значениях k=0; 1; 2; …n-1.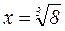 , представим число 8 в тригонометрической форме.
, представим число 8 в тригонометрической форме.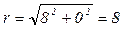 ; j=0; 8=8× (cos0+i sin0)
; j=0; 8=8× (cos0+i sin0)
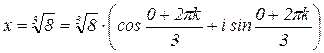
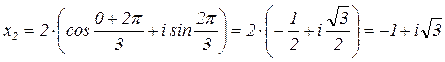


 е, аналогично
е, аналогично 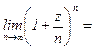 еz, где z=a+вi; еz=ea+вi
еz, где z=a+вi; еz=ea+вi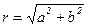 .
.
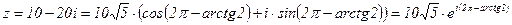
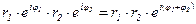 .
.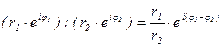 .
.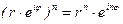 .
.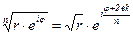 , где k=0; 1; 2; …n-1.
, где k=0; 1; 2; …n-1.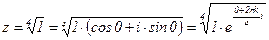 ;
;