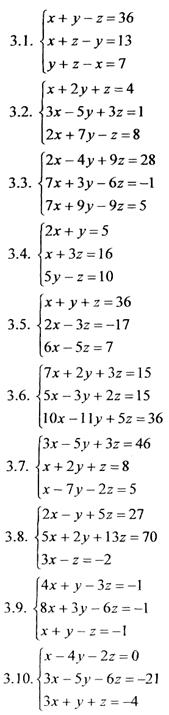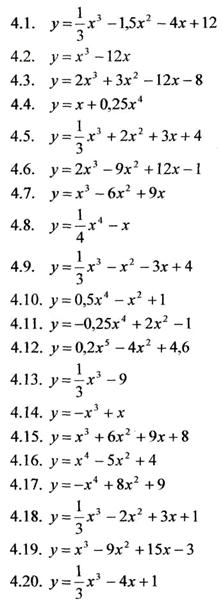Решить задачу (кривые 2-го порядка)
2.1. Дано уравнение гиперболы 7х2–9у2–63=0. Написать уравнение в каноническом виде и найти все элементы гиперболы, ее эксцентриситет и уравнения асимптот. 2.2. Написать уравнение эллипса, если малая ось равна 10, а расстояние между фокусами равно 12 (сделать рисунок). 2.3. Написать уравнение гиперболы и ее асимптот, если мнимая ось равна 6, а эксцентриситет равен 2.4. Дано уравнение параболы у=х2–6х+2. Найти все элементы параболы и сделать чертеж. 2.5. Найти координаты центра и диаметр окружности 2х2+2у2–6х+10у=33 (сделать чертеж). 2.6. Дано уравнение гиперболы 9х2–4у2=36. Найти элементы этой параболы, эксцентриситет, составить уравнения асимптот гиперболы. 2.7. Написать уравнение эллипса, если фокусы имеют координаты (±4; 0), а длина большей оси равна 10 (сделать чертеж). 2.8. Написать уравнение окружности, если диаметр АВ имеет координаты концов (-2; 2) и (7; -7) (сделать чертеж). 2.9. Написать уравнение параболы, у которой вершина лежит в начале координат, а уравнение директрисы х+3=0 (сделать чертеж). 2.10. Дано уравнение эллипса 2х2+3у2=6. Найти его элементы, эксцентриситет (сделать чертеж). 2.11. Написать уравнение эллипса, у которого эксцентриситет равен 2.12. Написать уравнение гиперболы и ее асимптот, если действительная ось равна 8, а эксцентриситет равен 1, 25 (сделать чертеж). 2.13. Написать уравнение эллипса, если расстояние одного из фокусов до вершин на большей оси равны 2 и 10 единиц. 2.14. Найти расстояние от центра окружности х2+у2–6х+4у+4=0 до точки А(-5; 3). 2.15. Найти элементы и эксцентриситет эллипса 2.16. Найти элементы и эксцентриситет эллипса 2.17. Парабола с вершиной в начале координат, симметричная относительно оси ОХ проходит через точку (1; 2). Написать ее уравнение и сделать чертеж. 2.18. Найти элементы параболы (у–5)2+8х–4=0 (сделать чертеж). 2. 19. Найти элементы, эксцентриситет, уравнение асимптот гиперболы 2.20. Найти элементы, эксцентриситет эллипса
Задание № 3 (4 час.) Исследовать систему и решить ее двумя способами по выбору.
Задание № 4 (8 час.) Исследовать функцию и построить ее график.
Задание № 5 (4 час.)
Преобразовать в тригонометрическую и показательную формы комплексное число. Задание № 6. Теория (8 час.) (Вопросы к зачету) 1. Метод координат. Формы преобразования координат. Расстояние между двумя точками на плоскости. Деление отрезка в данном отношении. Привести примеры. 2. Полярные координаты. Связь между полярными и прямоугольными координатами. Привести примеры. 3. Векторное произведение векторов, его свойства, вычисление и применение. Привести примеры. 4. Смешанное произведение векторов, его свойства, способы вычисления. Приложения смешанного произведения. Привести примеры. 5. Уравнение линии. Уравнение прямой в общем виде и в отрезках. 6. Расстояние от точки до прямой. Ориентация плоскости. Уравнение биссектрисы угла. Привести примеры. 7. Угол между прямыми. Вычисление угла между прямыми различными способами. Привести примеры. 8. Взаимное расположение двух прямых на плоскости. Условия параллельности и перпендикулярности прямых. 9. Взаимное расположение прямой и плоскости в пространстве. Выражение этих расположений через координаты. 10. Взаимное расположение двух плоскостей в пространстве. Выражение этого расположения через координаты. (a^β, aÇ β =a, a=β, a║ β) 11. Уравнение плоскости, проходящей через данную точку с заданным нормальным вектором. Уравнение плоскости в общем виде. Расположение плоскости относительно координатных плоскостей. 12. Уравнение плоскости, проходящей через три точки. Уравнение плоскости в отрезках. Привести примеры. 13. Понятие функции. Способы ее задания. Виды функций. Привести примеры. 14. Геометрический смысл производной. Вывод уравнения касательной и нормали к графику функции. Привести примеры. 15. Дифференциал функции. Геометрический смысл дифференциала. Приложение дифференциала к приближенным вычислениям. Привести примеры. 16. Дифференциал дуги плоской кривой. 17. Кривизна. Радиус кривизны. 18. Приближенные способы интегрирования. 19. Приложение определенного интеграла к вычислению площади криволинейной фигуры. 20. Приложение определенного интеграла к вычислению объема тела вращения и объема тела по поперечному сечению тела. 21.Приложение определенного интеграла к вычислению длины дуги.
|

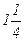 (сделать чертеж).
(сделать чертеж). , а абсцисса одного из фокусов равна
, а абсцисса одного из фокусов равна 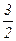 (сделать чертеж).
(сделать чертеж).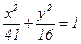 .
.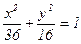 (сделать чертеж).
(сделать чертеж).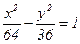 .
.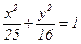 (сделать чертеж).
(сделать чертеж).