Определение:
 Производной функции f/(x) или у/ от данной функции у=f(x) называется предел отношения приращения функции к приращению аргумента, когда последний стремится к нулю.
Производной функции f/(x) или у/ от данной функции у=f(x) называется предел отношения приращения функции к приращению аргумента, когда последний стремится к нулю.
Чтобы найти производную функции, необходимо выполнить следующие шаги:

1. f(x+  x)=… найти наращенное зная функцию.
x)=… найти наращенное зная функцию.
2.  y=f(x+
y=f(x+  x)-f(x)=… - приращение функции.
x)-f(x)=… - приращение функции.
3.  =
=  =… - отношение
=… - отношение  у к
у к  х.
х.
4. y/=lim  x
x  0,
0,  =lim
=lim  x
x  0,
0,  =… - предел этого отношения при
=… - предел этого отношения при  x
x  0.
0.
Этот алгоритм нахождения производной называется дифференцированием функции.
Понятие производной является одним из основных и важнейших понятий математического анализа. К понятию производной приходится обращаться при решении целого ряда задач по физике, механике и геометрии, связанных с изучением скорости некоторого процесса.
Так при движении материальной точки по прямой при неравномерном движении проёденный путь будет зависеть от времени. За период времени  t, точка пройдет путь
t, точка пройдет путь  S при достаточно малом значении
S при достаточно малом значении  t скорость можно считать постоянной и тогда Vср=
t скорость можно считать постоянной и тогда Vср= 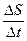 при
при  t
t  0 Vср
0 Vср  Vсигн
Vсигн  Vсигн=lim
Vсигн=lim  t
t  0, Vcp = lim
0, Vcp = lim  t
t  0,
0, 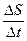 =S/
=S/  |S/(t)=V*в данный момент времени.
|S/(t)=V*в данный момент времени.
 Формулу * называют физическим смыслом производной, то есть производная – есть скорость изменения функции в данной точке. (или мгновенная скорость движения). Производная функции имеет и геометрический смысл.
Формулу * называют физическим смыслом производной, то есть производная – есть скорость изменения функции в данной точке. (или мгновенная скорость движения). Производная функции имеет и геометрический смысл.
Пусть y=f(x) имеет x0, f(x0), x+  x, и f(x0+
x, и f(x0+  x). М0 и М соответствую x0 и х и лежат на графике у=f(x), тогда (М0М) – секущая. Из
x). М0 и М соответствую x0 и х и лежат на графике у=f(x), тогда (М0М) – секущая. Из  М0NM имеем: tg
М0NM имеем: tg 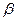 =
=  =
=  (1)
(1)
Пусть точка М, двигаясь по кривой неограниченно близко приближается к точке М0. Тогда будут происходить следующие процессы:
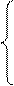 (М0М)
(М0М)  (М0К) – касательной к графику у=f(x) в точке М0.
(М0К) – касательной к графику у=f(x) в точке М0.
М  М0
М0 
 х
х  0.
0.
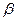
 d
d  tg
tg 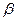
 tgd
tgd

 Производной функции f/(x) или у/ от данной функции у=f(x) называется предел отношения приращения функции к приращению аргумента, когда последний стремится к нулю.
Производной функции f/(x) или у/ от данной функции у=f(x) называется предел отношения приращения функции к приращению аргумента, когда последний стремится к нулю.
 x)=… найти наращенное зная функцию.
x)=… найти наращенное зная функцию. =
=  =… - отношение
=… - отношение  0,
0, 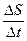 при
при  Vсигн=lim
Vсигн=lim  Формулу * называют физическим смыслом производной, то есть производная – есть скорость изменения функции в данной точке. (или мгновенная скорость движения). Производная функции имеет и геометрический смысл.
Формулу * называют физическим смыслом производной, то есть производная – есть скорость изменения функции в данной точке. (или мгновенная скорость движения). Производная функции имеет и геометрический смысл.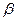 =
=  =
=  (М0М)
(М0М) 


