Розрахунок довжини нитки в петлі за глибиною кулірування
Довжину нитки в петлі визначатимемо з умови отримання її мінімальної довжини, для чого голку потрібно розміщувати точно посередині в зазорі між платинами. Довжина нитки (рисунок 8.1) складається із суми довжин окремих ділянок петлі, виміряних по середній лінії нитки:
У силу симетричності розрахункової моделі петлі
Визначимо кожний доданок виразу (2). Визначаємо довжину l 12 прямолінійної ділянки петлі (відстань між точками 2-3):
де р – товщина платини; rр – радіус закруглення платини. Визначаємо довжину прямолінійної ділянки петлі при куліруванні l 34 (відстань між точками 3-4):
де О 1 О 2 – відстань між центром закруглення платини та центром перерізу гачка голки (див. рисунок 8.1); r 1 – радіус огинання ниткою закруглення платини, виміряний по середній лінії нитки (див. рисунок 8.1); r 2 – радіус огинання ниткою головки голки, виміряний по середній лінії нитки; Визначаємо радіус r 1 огинання ниткою платини (рисунок 8.1):
Рисунок 8.1. Розрахункова схема для визначення довжини нитки при куліруванні
Визначаємо радіус r 2 огинання ниткою голки:
Визначаємо відстань h між центрами О 1 та О 2, виміряну за напрямом руху голки (на рисунку 8.1 голка рухається по вертикалі):
Визначаємо відстань О 1 О 2:
Для визначення довжин криволінійних ділянок нитки при куліруванні l 23 та l 45 спочатку знайдемо значення кутів φ1, φ2, θ, α1, α2:
Визначаємо кут α1 огинання ниткою платини та кут α2 огинання ниткою голки:
Визначаємо довжини криволінійних ділянок нитки l 23 та l 45 при куліруванні:
|

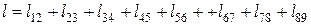 . (1)
. (1)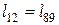 ,
, 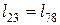 ,
,  і
і 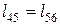 , тому вираз (1) перепишеться таким чином:
, тому вираз (1) перепишеться таким чином: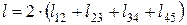 . (2)
. (2)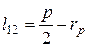 , (3)
, (3)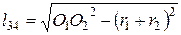 . (4)
. (4)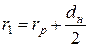 . (5)
. (5)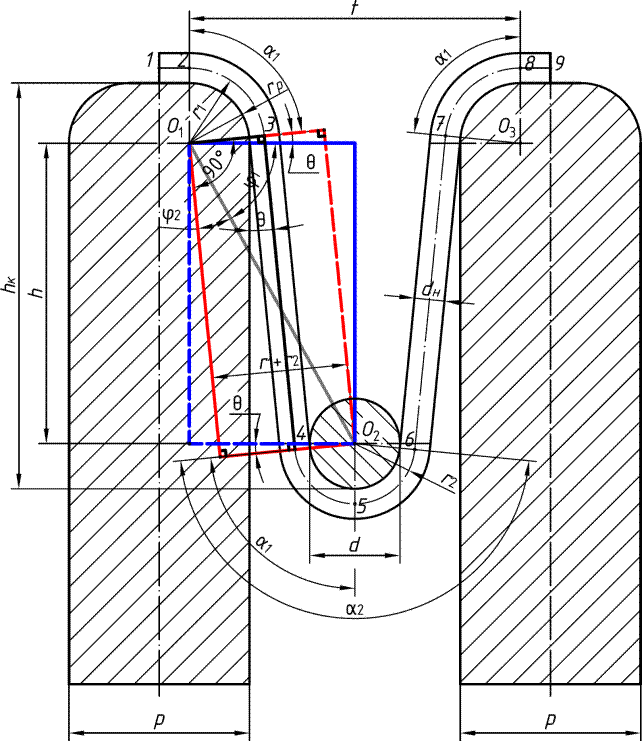
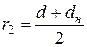 . (6)
. (6)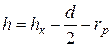 . (7)
. (7)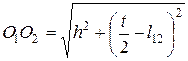 . (8)
. (8)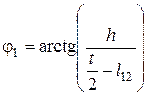 ; (9)
; (9)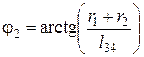 ; (10)
; (10)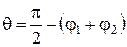 . (11)
. (11)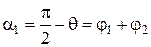 ; (12)
; (12)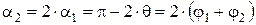 . (13)
. (13)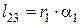 ; (14)
; (14)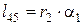 . (15)
. (15)


