Пример 3.1
Используя способ последовательных разностей, определить, присутствует ли систематическая погрешность в ряду результатов наблюдений, приведенных во втором столбце таблицы 3.2. Таблица 3.2 Результаты наблюдений
Для приведенного ряда результатов вычисляем: среднее арифметическое оценку дисперсии S2[х]=2,58/10=0,258; значение Q2[х]=4,12/(2·10)=0,206; критерий Аббе ν=0,206/0,258=0,8.
Как видно из таблицы 3.1, для всех уровней значимости (q=0,001; 0,01 и 0,05) при n=11 имеем ν>νq, т.е. подтверждается нулевая гипотеза о постоянстве центра группирования. Следовательно, условия измерений для приведенного ряда оставались неизменными, и систематических расхождений между результатами наблюдений нет. Задача Используя способ последовательных разностей, определить, присутствует ли систематическая погрешность в ряду результатов наблюдений, приведенных в таблице 3.3. Таблица 3.3 Результаты измерений
4. Вероятностное описание случайных погрешностей
Когда при проведении в одинаковых условиях повторных измерений одной и той же постоянной величины получаем результаты, отличающиеся друг от друга, это свидетельствует о наличии в них случайных погрешностей. Эта погрешность возникает вследствие одновременного воздействия на результат многих случайных возмущений и сама является случайной величиной. Для установления вероятностных (статистических) закономерностей появления случайных погрешностей и количественной оценки результата измерений и его случайной погрешности используются методы теории вероятностей и математической статистики. Для характеристики свойств случайной величины в теории вероятностей используют понятие закона распределения вероятностей случайной величины. В метрологии преимущественно используется дифференциальная форма – закон распределения плотности вероятностей случайной величины. Рассмотрим формирование дифференциального закона. 1. Проведем n измерений одной величины Х. 2. Получим группу наблюдений х1; х2,…,хn. 3. Расположим результаты в порядке возрастания от хmin до хmax. 4. Найдем размах ряда L=хmax - хmin. 5. Разделим размах ряда на k равных интервалов ∆l=L/k. 6. Подсчитаем количество наблюдений nk, попадающих в каждый интервал. 7. Изобразим полученные результаты графически (по оси абсцисс – значения физической величины с границами интервалов; по оси ординат – относительная частота попаданий nk/n). 8. Достроив по полученным точкам соответствующие прямоугольники, получим гистограмму (рис.4.1), дающую представление о плотности распределения результатов наблюдений в данном опыте. Пример 4.1. Построить гистограмму по данным приведенным ниже. n =50 измерений.
Рис.4.1. Гистограмма
Если распределение случайной величины статистически устойчиво, то можно ожидать, что при повторных сериях наблюдений той же величины в тех же условиях, относительные частоты попаданий в каждый интервал будут близки к первоначальным. Следовательно, по гистограмме можно предсказывать распределение результатов измерений по интервалам. При бесконечном увеличении числа наблюдений n→∞; и бесконечном уменьшении ширины интервалов Δl→0, ступенчатая кривая, огибающая гистограмму, перейдет в плавную кривую f(x), которая называется кривой плотности распределения вероятностей случайной величины (рис.4.2), а уравнения ее описывающие дифференциальным законом распределения.
Рис.4.2. Кривая плотности распределения вероятностей
Кривая плотности распределения вероятностей всегда неотрицательна и подчинена условию нормирования в виде:
Если известен закон распределения случайной величины f(x), то вероятность Р ее попадания в интервал от х1 до х2 :
Числовые характеристики случайных величин вычисляются по следующим формулам: · среднее арифметическое значение исправленных результатов наблюдений
· смещенная (S*) и несмещенная (S) среднеквадратическая погрешность ряда измерений
· среднеквадратическая погрешность среднеарифметического значения:
Методика проверки гипотезы о том, что результаты наблюдений распределены нормально, зависит от числа наблюдений: - если n≥50, используют критерий χ2 Пирсона; - если 15<n<50, то используют составной критерий; - если n≤15, то гипотезу не проверяют (в этом случае данная методика обработки результатов может применяться, если априорно известно, что наблюдения распределены нормально). Рассмотрим методику проверки гипотезы о нормальном законе распределения результатов наблюдений при 15<n<50. В этом случае используется составной критерий, включающий в себя критерий 1 и критерий 2. Гипотеза считается не противоречащей результатам наблюдений при уровне значимости Критерий 1. Вычисляют значение d по формуле :
Затем задаются уровнем значимости Критерий 2. Определяют значение m:
Затем задаются уровнем значимости Гипотеза, удовлетворяет критерию 2, если Таблица 4.1 Значения d1 и d2
Таблица 4.2 Значения z
Задача По данным, приведенным в таблице 3.3. проверить гипотезу о согласованности эмпирического и теоретического распределения по составному критерию. 5. Грубые погрешности и методы их исключения
Грубая погрешность или промах – это погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда. Источником грубых погрешностей являются резкие изменения условий измерения и ошибки, допущенные оператором. Вопрос о том, содержит ли результат наблюдений грубую погрешность, решается методами проверки статистических гипотез. Проверяемая гипотеза состоит в утверждении, что результат наблюдения хi не содержит грубой погрешности, т.е. является одним из значений измеряемой величины. Пользуясь определенными статистическими критериями, пытаются опровергнуть выдвинутую гипотезу. Если это удается, то результат измерений рассматривают как содержащий грубую погрешность и его исключают. Для выявления грубых погрешностей задаются вероятностью q (уровнем значимости) того, что сомнительный результат действительно мог иметь место в данной совокупности результатов измерений. Критерий «трех сигм» применяется для результатов измерений, распределенных по нормальному закону. По этому критерию считается, что результат, возникающий с вероятностью q≤0,003, маловероятен и его можно считать промахом, если Данный критерий надежен при n ≥20…50 и выполним только для нормального закона распределения. Критерий Романовского применяется, если число измерений n<20. При этом выполняется отношение
и сравнивается с критерием βТ, выбранным в таблице 5.1. Если β≥βТ, то результат xi считается промахом и отбрасывается. Таблица 5.1 Значения критерия Романовского β=f(n)
Вариационный критерий Диксона – удобный и достаточно мощный (с малыми вероятностями ошибок). При его применении полученные результаты наблюдений записывают в вариационный возрастающий ряд x1; x2;…;xn (x1< x2<…< xn). Критерий Диксона определяется следующим образом:
Критическая область для этого критерия Р(КД>Zq)=q. Значения Zq приведены в таблице 5.2. Таблица 5.2 Значения критерия Диксона
|

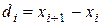



 =154,0/11=14;
=154,0/11=14; 17
17


 . (4.1)
. (4.1) . (4.2)
. (4.2) , которое принимается за результат измерения, если подтверждается гипотеза о нормальном распределении результатов наблюдений и ряд наблюдений не содержит промахов:
, которое принимается за результат измерения, если подтверждается гипотеза о нормальном распределении результатов наблюдений и ряд наблюдений не содержит промахов: ; (4.3)
; (4.3) ; (4.4)
; (4.4) . (4.5)
. (4.5) . (4.6)
. (4.6) , если требования критерия 1 выполняются при уровне значимости
, если требования критерия 1 выполняются при уровне значимости  , а критерия 2 – при уровне значимости
, а критерия 2 – при уровне значимости  . Рекомендуются значения уровня значимости
. Рекомендуются значения уровня значимости  от 0,02 до 0,10.
от 0,02 до 0,10. . (4.7)
. (4.7)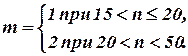
 , удовлетворяющих неравенству
, удовлетворяющих неравенству 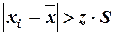 .
. .
. где
где  - оценка СКО измерений.
- оценка СКО измерений. (5.1)
(5.1) . (5.2)
. (5.2)


