Пример 7.1
Оценить погрешность результата измерения напряжения U=0,9 В на сопротивлении R=4 Ом, выполненного вольтметром класса точности 0,5 с верхним пределом измерения UN=1,5 В и внутренним сопротивлением RV=1000 Ом. Известно, что дополнительные погрешности показаний вольтметра из-за магнитного поля и температуры не превышают соответственно ΘМП= ±0,75% и ΘТ= ±0,3% допускаемой предельной погрешности. Решение Методическая погрешность измерения напряжения составляет
где Uv – показания вольтметра, В; U – измеряемое напряжение, В.
Данная погрешность является систематической и должна быть внесена в результат в виде поправки q=-δUм=-0,4% или в абсолютной форме Результат измерения с учетом поправки Предел допускаемой относительной погрешности вольтметра на отметке 0,9 В составляет где γ – относительная приведенная погрешность прибора.
Следовательно, ΘV= ±0,83%. Поскольку основная и дополнительная погрешности заданы своими граничными значениями, то они могут рассматриваться как неисключенные систематические погрешности и соответственно суммироваться. При доверительной вероятности 0,95 доверительная граница неисключенной систематической погрешности согласно формуле (7.3)
В абсолютной форме Окончательный результат измерения записывается в виде U=(0,904±0,012) В при Р=0,95. Задача Необходимо измерить напряжение постоянного тока на выходе активного двухполюсника в режиме холостого хода. Используя данные, приведенные в таблице 7.1, оценить погрешность результата однократного измерения напряжения U на сопротивлении R, учитывая дополнительную температурную погрешность. В соответствии с ГОСТом 22261-82 дополнительная температурная погрешность для данного типа приборов не превышает основной при изменении температуры на каждые 10ºС. Таблица 7.1 Результаты измерений
8. Обработка результатов косвенных измерений
При косвенных измерениях искомое значение величины находят расчетом на основе измерения других величин, связанных с измеряемой величиной известной зависимостью А =f(а1, …, аn). (8.1) Результатом косвенного измерения является оценка величины А, которую находят подстановкой в формулу (8.1) оценок аргументов аi. При сложной функции (8.1) и в особенности, если это функция нескольких аргументов, отыскание закона распределения погрешности результата связано со значительными математическими трудностями. В основе приближенного оценивания погрешности нелинейных косвенных измерений лежит линеаризация функции (8.1) и дальнейшая обработка результатов, как при линейных измерениях. Применяя некоторые упрощения, получим несколько простых правил оценивания погрешности результата косвенного измерения. Правило 1. Погрешности в суммах и разностях. Если а1 и а2 измерены с погрешностями Δа1 и Δа2 и измеренные значения используются для вычисления суммы или разности А=а1± а2, то суммируются абсолютные погрешности (без учета знака): ΔА=Δа1 + Δа2. (8.2) Правило 2. Погрешности в произведениях и частных. Если измеренные значения а1 и а2 используются для вычисления А= а1·а2 или А = а1 /а2, то суммируются относительные погрешности δА = δа1 + δа2. (8.3) где δа = Δа/а. Правило 3. Измеренная величина умножается на точное число. Если а используется для вычисления произведения А = В а, в котором В не имеет погрешности, то δА = │ В│δа. (8.4) Правило 4. Возведение в степень. Если а используется для вычисления степени А = аn, то δА = nδа. (8.5) Правило 5. Погрешность в произвольной функции одной переменной. Если а используется для вычисления функции А(а), то
Использование правил позволяет получить не слишком завышенную оценку предельной погрешности результата нелинейного косвенного измерения при не слишком большом числе аргументов (m < 5 ).
|

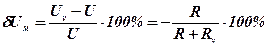 ,
,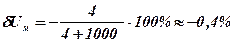 .
. .
.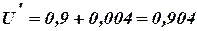 В.
В.
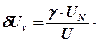 ,
, .
. ,
, .
. .
. . (8.6)
. (8.6)


