Пример 6.1
Определить наиболее достоверное значение напряжение U постоянного тока, измеренного компенсатором постоянного тока и предельную погрешность найденного значения при заданной доверительной вероятности Р=0,99. Результаты 13 равноточных измерений следующие: 100,08 мВ; 100,09 мВ; 100,07 мВ; 100,10 мВ; 100,05 мВ; 100,06 мВ; 100,04 мВ; 100,06 мВ; 99,95 мВ; 99,92 мВ; 100,02 мВ; 99,98 мВ; 99,97 мВ. Решение Среднее арифметическое значение ряда измерений Сумма остаточных погрешностей Среднеквадратическая погрешность ряда измерений
Среднеквадратическая погрешность среднеарифметического значения
Доверительный интервал Наиболее достоверное значение напряжения U=(100,03±0,04) мВ, Р=0,98. Задача По результатам, полученным при решении задачи №5 (с исключенными промахами), провести обработку результатов измерений и определить наиболее достоверное значение напряжения и предельную погрешность найденного значения.
7. Прямые однократные измерения
Для производственных процессов характерны однократные измерения. За результат прямого однократного измерения принимается полученная величина. При определении доверительных границ погрешности результата измерения доверительная вероятность принимается равной 0,95. Методика обработки результатов прямых однократных измерений приведена в рекомендациях МИ 1552-86 «ГСИ. Измерения прямые однократные. Оценивание погрешностей результатов измерений». Абсолютная погрешность результата измерения Δ; (погрешность измерения) определяется тремя составляющими: инструментальной Δи, методической Δм и погрешности отсчитывания Δотс. В большинстве случаев полагают, что
По нормируемым метрологическим характеристикам можно определить только предельные значения составляющих погрешности Δi погрешности измерения В этом случае результат измерения можно представить в виде х±Δ; Р=1, (7.2) где х – значение измеряемой величины; Δ; – предел погрешности результата измерения; Р – доверительная вероятность. При наличии нескольких систематических погрешностей, заданных своими границами ±Θi или доверительными границами ±Θi(Р), доверительная граница результата может быть рассчитана по формуле;
где Θi(Pj) – доверительная граница i -й неисключенной систематической погрешности, соответствующая доверительной вероятности Pj; kj - коэффициент, зависящий от Pj и определяемый так же, как и коэффициент k; k=k(m:P) – коэффициент, равный 0,95 при Р=0,9 и 1,1 при Р=0,95 (при других доверительных вероятностях он определяется в соответствии с ГОСТ 8.207-76). В практике имеет место приближенное оценивание погрешности полученного результата на основе метрологических характеристик, приведенных в нормативно-технической документации на используемые средства измерений. В простейшем случае, когда влияющие величины соответствуют нормальным условиям, погрешность результата прямого однократного измерения равна пределу основной погрешности средства измерений, определяемой по нормативно-технической документации. Доверительная вероятность подразумевается равной 0,95.
|

 .
. , что свидетельствует о правильности расчета
, что свидетельствует о правильности расчета  .
. .
.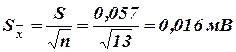 .
. .
. . (7.1)
. (7.1) .
. (7.3)
(7.3)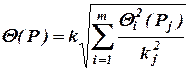 (7.4)
(7.4)


