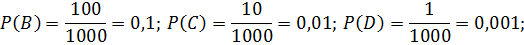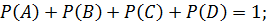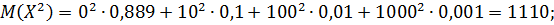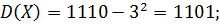Параграф 3. Дискретная случайная величина
Ряд распределения дискретной случайной величины:
Свойства закона распределения случайной дискретной величины: Свойство 1. Сумма вероятностей всех возможных значений, которые может принять дискретная случайная величина, равна единице.
Доказательство. События Свойство доказано. Закон распределения дискретной случайной величины может быть изображен графически, если по оси абсцисс откладывать значения случайной величины, а по оси ординат соответствующие их вероятности. Соединение полученных точек образует ломаную, называемую полигоном распределения вероятностей дискретной случайной величины. Математическим ожиданием или средним значением
Свойства математического ожидания дискретной случайной величины Свойство 1. Математическое ожидание постоянной величины равно самой постоянной:
Доказательство. Постоянную величину
Свойство доказано. Свойство 2. Постоянный множитель можно выносить за знак математического ожидания:
Доказательство. Так как случайная величина
Свойство доказано. Свойство 3. Математическое ожидание суммы дискретных случайных величин равна сумме математических ожиданий этих дискретных случайных величин:
Доказательство. Свойство доказано. Свойство 4. Математическое ожидание произведения независимых дискретных случайных величин равна произведению этих дискретных случайных величин:
Доказательство. Свойство доказано. Свойство 5. Если все значения дискретной случайной величины увеличить или уменьшить на постоянную
Доказательство. Учитывая свойства 3 и 1 математического ожидания, получим:
Свойство доказано. Свойство 6. Математическое ожидание отклонения дискретной случайной величины от ее математического ожидания равна нулю:
Доказательство. Пусть постоянная
Свойство доказано. Дисперсией или разбросом
Свойства дисперсии дискретной случайной величины Свойство 1. Дисперсия постоянной величины равна нулю:
Доказательство. Учитывая свойство 1 математического ожидания, получим:
Свойство доказано. Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат:
Доказательство. Учитывая свойство 2 математического ожидания, получим:
Свойство доказано. Свойство 3. Дисперсия дискретной случайной величины равна разности между математическим ожиданием квадрата дискретной случайной величины и квадратом ее математического ожидания:
Докозательство. Учитывая свойства 2 и 3 математического ожидания получим:
Свойство доказано. Свойство 4. Дисперсия суммы независимых дискретных случайных величин равна сумме их дисперсий:
Доказательство.
Свойство доказано. Свойство 5. Дисперсия разности независимых дискретных случайных величин равна сумме их дисперсий:
Докозательство. Свойство доказано. Средним квадратическим отклонением или стандартом
Пример 1. В денежной лотерее 1 выйгрыш в 1000 рублей, 10 выйгрышей по 100 рублей и 100 выйгрышей по 10 рублей, при общем числе билетов 1000. Найти закон распределения случайного выйгрыша Решение. Возможные значения для Вероятности возможных значений
События
|




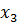

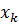


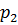



 , состоящие в том, что в результате испытания случайная величина
, состоящие в том, что в результате испытания случайная величина  , являются несовместимыми и единственно возможными, так как в таблице перечислены все возможные значения случайной величины, а значит, образуют полную группу. Следовательно, сумма их вероятностей равна единице.
, являются несовместимыми и единственно возможными, так как в таблице перечислены все возможные значения случайной величины, а значит, образуют полную группу. Следовательно, сумма их вероятностей равна единице. дискретной случайной величины
дискретной случайной величины 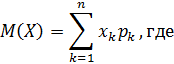
 – математическое ожидание дискретной случайной величины
– математическое ожидание дискретной случайной величины  – возможное значение дискретной случайной величины
– возможное значение дискретной случайной величины 
 можно рассматривать как величину, принимающую значение
можно рассматривать как величину, принимающую значение 

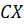 принимает значения
принимает значения  , то:
, то:


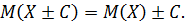
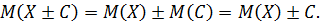

 . Тогда, используя свойство 5, получим:
. Тогда, используя свойство 5, получим:
 дискретной случайной величины
дискретной случайной величины 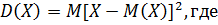
 – дисперсия дискретной случайной величины
– дисперсия дискретной случайной величины 

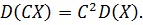




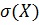 дискретной случайной величины
дискретной случайной величины 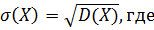
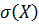 – среднее квадратическое отклонение дискретной случайной величины
– среднее квадратическое отклонение дискретной случайной величины  .
. – вытянут лотерейный билет в 0 рублей;
– вытянут лотерейный билет в 0 рублей; – вытянут лотерейный билет в 10 рублей;
– вытянут лотерейный билет в 10 рублей;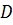 – вытянут лотерейный билет в 1000 рублей.
– вытянут лотерейный билет в 1000 рублей. образуют полную группу несовместимых и равновозможных событий.
образуют полную группу несовместимых и равновозможных событий.
 ;
;  ;
;  ;
;  ;
;