Параграф 7. Теоремы произведения вероятностей
События называются независимыми, если вероятность каждого из них не зависит от того, появилось другое событие или нет. События называются зависимыми, если вероятность появления каждого из них зависит от того, появилось другое или нет. Условной вероятностью события Условная вероятность обозначается через Теорема 1. Вероятностью произведения независимых событий равна произведению вероятностей этих событий:
Доказательство. Пример 1. Найти вероятность одновременного поражения цели двумя орудиями, если вероятность поражения цели первым орудием равна 0,8, а вторым 0,7. Решение.
События
Ответ. Теорема 2. Вероятность произведения зависимых событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что предыдущее событие уже произошло.
Доказательство. Пример 2. В урне находятся 2 белых и 3 черных шара. По очереди вынимают два шара, не возвращая их обратно. Найти вероятность того, что вынутые шары оба белые. Решение.
События
Ответ:
|
двух зависимых событий 
и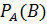 
.
; 
;
.
; 
; 
; 
;
.
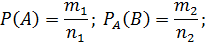
