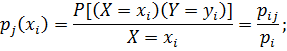Распределение двумерной дискретной случайной величины:
Свойства закона распределения двумерной дискретной случайной величины:
Свойство 1. Сумма вероятностей всех возможных значений, которые может принять дискретная многомерная случайная величина, равна единице:
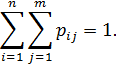
Доказательство.
События 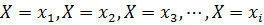 и
и 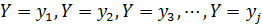 , состоящие в том, что в результате испытания случайная величина
, состоящие в том, что в результате испытания случайная величина  примет соответственно значения
примет соответственно значения  и
и 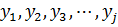 , являются несовместимыми и единственно возможными, так как в таблице перечислены все возможные значения случайной величины, а значит, образуют полную группу. Следовательно, сумма их вероятностей равна единице.
, являются несовместимыми и единственно возможными, так как в таблице перечислены все возможные значения случайной величины, а значит, образуют полную группу. Следовательно, сумма их вероятностей равна единице.
Свойство доказано.
Свойство 2. Чтобы по таблице распределения найти вероятность того, что одномерная величина  или
или 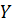 принимает определенное значение, надо просуммировать вероятности из соответствующей этому значению строки или столбца данной таблицы:
принимает определенное значение, надо просуммировать вероятности из соответствующей этому значению строки или столбца данной таблицы:
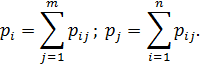
Доказательство.
Распределение одномерной дискретной случайной величины  можно получить, вычислив вероятность события
можно получить, вычислив вероятность события  как сумму вероятностей несовместимых событий:
как сумму вероятностей несовместимых событий:
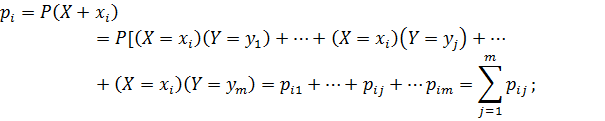
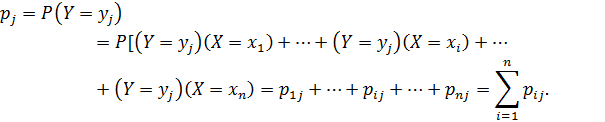
Свойство доказано.
Свойство 3. Условные распределения дискретных случайных величин  и
и 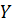 равны:
равны:
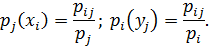
Доказательство. Зафиксируем значение  , то полученное распределение случайной величины
, то полученное распределение случайной величины  называется условным распределением
называется условным распределением  при условии
при условии  . Вероятности
. Вероятности  этого распределения будут условными вероятностями события
этого распределения будут условными вероятностями события  , при условии, что событие
, при условии, что событие  уже произошло. Из определения условной вероятности:
уже произошло. Из определения условной вероятности:
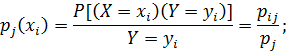
Зафиксируем значение  , то полученное распределение случайной величины
, то полученное распределение случайной величины 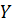 называется условным распределением
называется условным распределением 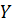 при условии
при условии  . Вероятности
. Вероятности  этого распределения будут условными вероятностями события
этого распределения будут условными вероятностями события  , при условии, что событие
, при условии, что событие  уже произошло. Из определения условной вероятности:
уже произошло. Из определения условной вероятности:
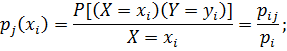
Свойство доказано.
Пример 1.

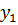

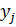





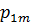

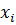




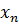
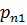



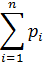
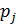
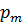
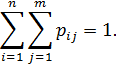
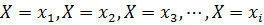 и
и 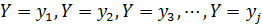 , состоящие в том, что в результате испытания случайная величина
, состоящие в том, что в результате испытания случайная величина  примет соответственно значения
примет соответственно значения  и
и 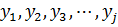 , являются несовместимыми и единственно возможными, так как в таблице перечислены все возможные значения случайной величины, а значит, образуют полную группу. Следовательно, сумма их вероятностей равна единице.
, являются несовместимыми и единственно возможными, так как в таблице перечислены все возможные значения случайной величины, а значит, образуют полную группу. Следовательно, сумма их вероятностей равна единице.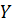 принимает определенное значение, надо просуммировать вероятности из соответствующей этому значению строки или столбца данной таблицы:
принимает определенное значение, надо просуммировать вероятности из соответствующей этому значению строки или столбца данной таблицы: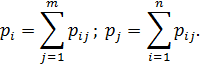
 как сумму вероятностей несовместимых событий:
как сумму вероятностей несовместимых событий: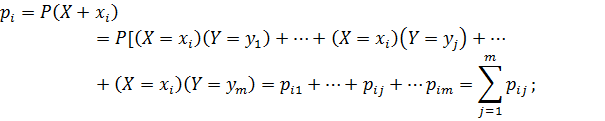
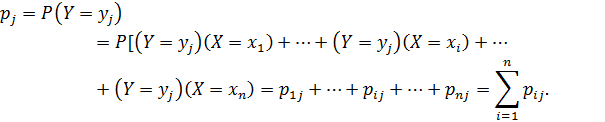
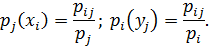
 , то полученное распределение случайной величины
, то полученное распределение случайной величины  этого распределения будут условными вероятностями события
этого распределения будут условными вероятностями события 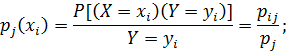
 этого распределения будут условными вероятностями события
этого распределения будут условными вероятностями события