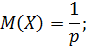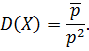Дискретная случайная величина  имеет закон распределения Пуассона, если она принимает бесконечное, но счетное множество значений с вероятностями:
имеет закон распределения Пуассона, если она принимает бесконечное, но счетное множество значений с вероятностями:
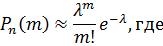
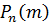 – вероятность того, что событие
– вероятность того, что событие  наступит
наступит  раз в
раз в 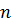 независимых испытаниях;
независимых испытаниях;
 – среднее значение числа появления события
– среднее значение числа появления события  при
при 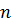 независимых испытаниях.
независимых испытаниях.
 – число независимых испытаний, в котором появилось событие
– число независимых испытаний, в котором появилось событие  ;
;
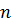 – общее число независимых испытаний.
– общее число независимых испытаний.
Ряд распределения закона Пуассона:
Теорема 1. Математическое ожидание и дисперсия случайной величины  , распределенной по закону Пуассона:
, распределенной по закону Пуассона:


Доказательство.
Теорема доказана.
Пример 1.
Параграф 3. Геометрическое распределение
Дискретная случайная величина  имеет геометрическое распределение, если она принимает бесконечное, но счетное множество значений с вероятностями:
имеет геометрическое распределение, если она принимает бесконечное, но счетное множество значений с вероятностями:
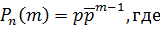
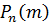 – вероятность того, что событие
– вероятность того, что событие  наступит
наступит  раз в
раз в 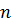 независимых испытаниях;
независимых испытаниях;
 – постоянная вероятность наступления события
– постоянная вероятность наступления события  ;
;
 – постоянная вероятность того, что событие
– постоянная вероятность того, что событие  не наступит.
не наступит.
Ряд геометрического распределения:
Теорема 1. Математическое ожидание и дисперсия случайной величины  , имеющей геометрическое распределение:
, имеющей геометрическое распределение:
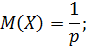
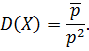
Доказательство.
Теорема доказана.
Пример 1.
Параграф 4. Гипергеометрическое распределение
Параграф 5. Равномерный закон распределения

 имеет закон распределения Пуассона, если она принимает бесконечное, но счетное множество значений с вероятностями:
имеет закон распределения Пуассона, если она принимает бесконечное, но счетное множество значений с вероятностями: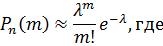
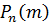 – вероятность того, что событие
– вероятность того, что событие  наступит
наступит  раз в
раз в 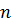 независимых испытаниях;
независимых испытаниях; – среднее значение числа появления события
– среднее значение числа появления события 
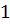









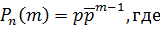
 – постоянная вероятность того, что событие
– постоянная вероятность того, что событие