Параграф 4. Функция распределения
Функцией распределения случайной величины
Свойства функции распределения: Свойство 1. Функция распределения случайной величины есть неотрицательная функция, заключенная между нулем и единицей:
Доказательство. Так как функция распределения выражает вероятность, то по 4 свойству вероятности:
Свойство доказано. Свойство 2. Функция распределения случайной величины есть неубывающая функция на всей числовой оси. Доказательство. Пусть
Так как вероятность Свойство доказано. Свойство доказано. Свойство 3. Вероятность попадания случайной величины в интервал, сегмент и полуинтервал с одними и теми же концами одинаковы и равны приращению их функции на этом интервале:
Доказательство. Используя формулу из 2 свойства функции распределения:
Доказательство. Свойство доказано. Свойство 4. Если возможные значения случайной величины принадлежат интервалу от
Доказательство.
Свойство доказано.
|
называется функция, выражающая для каждого возможного значения вероятность того, что случайная величина 
и 
точки числовой оси, причем 
. Рассмотрим два несовместимых события 
и 
. Тогда 
.
, то 
, т.е. 
неубывающая функция.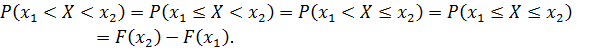
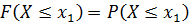Событие 
невозможно, следовательно, по 2 свойству вероятности его вероятность равна нулю. Событие 
достоверно, следовательно, по 1 свойству вероятности, его вероятность равна единице.
