Параграф 3. Классическое определение вероятности
События называются равновозможными, если в результате испытания по условии симметрии ни одно из этих событий не является объективно более возможным. Пример 1. Выпадение герба и выпадение цифры при одном бросании монеты; выпадение того или иного количества очков при одном бросании игральной кости являются равновозможными, так как обладают условиями симметрии; вытягивание карты из колоды так же является равновозможным событием. Несколько событий образуют полную группы событий для данного испытания, если его результатом становится хотя бы одно из них. Пример 2. Выпадение герба и выпадение цифры при одном бросании монеты; попадание в цель и промах при одном выстреле; выпадение того или иного количества очков при одном бросании игральной кости. События образующие полную группу несовместимых и равновозможных событий, называются элементарными событиями. Пример 3. Испытание: однократное бросание игральной кости. Событие Событие Пример 3. Испытание: однократное бросание игральной кости. Событие Вероятностью события
Пример 4. Найти вероятность выпадения цифры при одном бросании монеты. Решение.
События
Ответ: Свойства вероятности: Свойство 1. Вероятность достоверного события равна единице.
Доказательство. Достоверному событию должны благоприятствовать все
Свойство доказано. Свойство 2. Вероятность невозможного события равна нулю.
Доказательство. Невозможному событию не может благоприятствовать ни одно из элементарных событий, т.е.
Свойство доказано. Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.
Доказательство. Случайному числу благоприятствует лишь часть из общего числа
Свойство доказано. Свойство 4. Вероятность любого события:
Доказательство. Вероятность любого события есть сумма невозможного, случайного и достоверного событий, а значит и сумма их интервалов:
Свойство доказано.
|

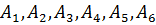 – появление одного, двух, трех, четырех, пяти и шести очков соответственно. События
– появление одного, двух, трех, четырех, пяти и шести очков соответственно. События  называется благоприятствующим событию
называется благоприятствующим событию  , если наступление события
, если наступление события  – появление двух, четырех, шести очков соответственно; событие
– появление двух, четырех, шести очков соответственно; событие 
 – вероятность события
– вероятность события  – число элементарных событий, благоприятствующих событию
– число элементарных событий, благоприятствующих событию 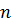 – число всех элементарных событий.
– число всех элементарных событий.
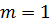 ;
;  ;
;
 .
.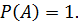
 :
:

 :
: