Деформации твердых тел могут быть весьма разнообразны (растяжение-сжатие, изгиб, кручение, сдвиг и т.д.). Но практически все они могут быть сведены к двум - растяжению-сжатию и сдвигу.
При одноосном растяжении материала увеличивается расстояние между молекулами тела в каком-то одном направлении. Выделим участок образца, имевший до деформации длину Dx. После деформации его длина станет равной Dx`. Величина Dx`-Dx равна удлинению. Относительная деформация участка равна  . Если относительная деформация одна и та же во всем образце, то говорят, что образец деформирован однородно. Если относительная деформация меняется от области к области, то говорят, что образец деформирован неоднородно. Более строго - деформация является характеристикой бесконечно малого участка среды. Ее определяют так. Отмечают смещения u(x) и u(x+dx) двух бесконечно близких точек при деформации. Относительная деформация в точке x равна
. Если относительная деформация одна и та же во всем образце, то говорят, что образец деформирован однородно. Если относительная деформация меняется от области к области, то говорят, что образец деформирован неоднородно. Более строго - деформация является характеристикой бесконечно малого участка среды. Ее определяют так. Отмечают смещения u(x) и u(x+dx) двух бесконечно близких точек при деформации. Относительная деформация в точке x равна  .
.



 Деформация сдвига возникает при неодинаковом смещении параллельных слоев вещества. Для определения относительной сдвиговой деформации выделим кубик вещества высоты Dx. Если при деформации разность смещений верхней и нижней граней равна Du, то относительная деформация сдвига кубика равна
Деформация сдвига возникает при неодинаковом смещении параллельных слоев вещества. Для определения относительной сдвиговой деформации выделим кубик вещества высоты Dx. Если при деформации разность смещений верхней и нижней граней равна Du, то относительная деформация сдвига кубика равна 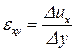 . При Dy®0 имеем
. При Dy®0 имеем  , т.е. определение точно такое же, как и определение одноосной деформации. Т.е. одноосную деформацию надо записать так:
, т.е. определение точно такое же, как и определение одноосной деформации. Т.е. одноосную деформацию надо записать так:  .
.
Деформация изгиба представляет собой неоднородно распределенную деформацию растяжения-сжатия. Одни слои в изогнутом стержне оказываются растянутыми, а другие - сжатыми.
 Деформация кручения представляет собой неоднородную сдвиговую деформацию (см. рисунок). При удалении от оси кручения деформация сдвига увеличивается.
Деформация кручения представляет собой неоднородную сдвиговую деформацию (см. рисунок). При удалении от оси кручения деформация сдвига увеличивается.

 При деформировании в твердых телах возникают силы упругости, стремящиеся расправить материал. При одноосном растяжении сила упругости действует перпендикулярно сечению стержня. В качестве характеристики возникающих сил вводится физическая величина, именуемая напряжением s. Напряжение в растягиваемом кубике определяется так:
При деформировании в твердых телах возникают силы упругости, стремящиеся расправить материал. При одноосном растяжении сила упругости действует перпендикулярно сечению стержня. В качестве характеристики возникающих сил вводится физическая величина, именуемая напряжением s. Напряжение в растягиваемом кубике определяется так:
 , (15)
, (15)
где DF - перпендикулярная к площадке сила, растягивающая (или сжимающая) кубик, DS - площадь грани, к которой приложена сила. При сдвиге сила действует не перпендикулярно, а параллельно плоскости грани. Сдвиговое напряжение, как и одноосное, определяется уравнением (15).
|
| Металл
| E ГПа
| G ГПа
|
| Металл
| E ГПа
| G ГПа
|
| 1
| Бериллий
| 300
| 145
| 4
| Медь
| 120
| 43
|
| 2
| Вольфрам
| 370
| 140
| 5
| Никель
| 210
| 74
|
| 3
| Железо
| 200
| 78
| 6
| Олово
| 50
| 18
|
Относительная деформация и возникающее в результате ее напряжение связаны законом Гука. В случае одноосного растяжения -
s=Ee, (16)
где E - модуль Юнга. В случае сдвига -
s=Ge, (17)
где G - модуль сдвига. Он не равен модулю Юнга. Характерные значения модулей приведены в таблице.

 . Если относительная деформация одна и та же во всем образце, то говорят, что образец деформирован однородно. Если относительная деформация меняется от области к области, то говорят, что образец деформирован неоднородно. Более строго - деформация является характеристикой бесконечно малого участка среды. Ее определяют так. Отмечают смещения u(x) и u(x+dx) двух бесконечно близких точек при деформации. Относительная деформация в точке x равна
. Если относительная деформация одна и та же во всем образце, то говорят, что образец деформирован однородно. Если относительная деформация меняется от области к области, то говорят, что образец деформирован неоднородно. Более строго - деформация является характеристикой бесконечно малого участка среды. Ее определяют так. Отмечают смещения u(x) и u(x+dx) двух бесконечно близких точек при деформации. Относительная деформация в точке x равна  .
.


 Деформация сдвига возникает при неодинаковом смещении параллельных слоев вещества. Для определения относительной сдвиговой деформации выделим кубик вещества высоты Dx. Если при деформации разность смещений верхней и нижней граней равна Du, то относительная деформация сдвига кубика равна
Деформация сдвига возникает при неодинаковом смещении параллельных слоев вещества. Для определения относительной сдвиговой деформации выделим кубик вещества высоты Dx. Если при деформации разность смещений верхней и нижней граней равна Du, то относительная деформация сдвига кубика равна 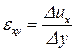 . При Dy®0 имеем
. При Dy®0 имеем  , т.е. определение точно такое же, как и определение одноосной деформации. Т.е. одноосную деформацию надо записать так:
, т.е. определение точно такое же, как и определение одноосной деформации. Т.е. одноосную деформацию надо записать так:  .
.
 Деформация кручения представляет собой неоднородную сдвиговую деформацию (см. рисунок). При удалении от оси кручения деформация сдвига увеличивается.
Деформация кручения представляет собой неоднородную сдвиговую деформацию (см. рисунок). При удалении от оси кручения деформация сдвига увеличивается.
 При деформировании в твердых телах возникают силы упругости, стремящиеся расправить материал. При одноосном растяжении сила упругости действует перпендикулярно сечению стержня. В качестве характеристики возникающих сил вводится физическая величина, именуемая напряжением s. Напряжение в растягиваемом кубике определяется так:
При деформировании в твердых телах возникают силы упругости, стремящиеся расправить материал. При одноосном растяжении сила упругости действует перпендикулярно сечению стержня. В качестве характеристики возникающих сил вводится физическая величина, именуемая напряжением s. Напряжение в растягиваемом кубике определяется так:  , (15)
, (15) 


