Задача 3. Изобразите характерный вид потенциальной энергии парного взаимодействия молекул. Приведите аргументы в пользу следующих утверждений:
а) существует равновесное расстояние между молекулами;
б) при малых отклонениях молекул от положения равновесия силу взаимодействия можно приближенно считать упругой.
Задача 4. Потенциальную энергию взаимодействия двух молекул приближенно описывают формулой Ленарда-Джонса  , где a и b – коэффициенты, определяемые из эксперимента.
, где a и b – коэффициенты, определяемые из эксперимента.
а) Используя потенциал Ленарда-Джонса, определите зависимость силы взаимодействия двух молекул от расстояния между ними.
Указание: воспользуйтесь связью между силой и потенциальной энергией взаимодействия F=-dU/dr.
б) Выразите равновесное расстояние между молекулами через коэффициенты a и b.
в) Покажите, что коэффициент жесткости квазиупругой связи между молекулами выражается через коэффициенты a и b следующим образом: 
Задача 5 [ Рейф 1.14 ]. Кристалл меди находится в равновесии при температуре 300°К. Атомная масса меди 64 г/моль, плотность 8,9×103кг/м3.
а) Оцените расстояние между атомами меди в кристалле. (Можно считать, что они расположены в вершинах кубической решетки).
б) Если внешняя сила F приложена к медному стержню с площадью поперечного сечения S и длиной L, то стержень удлиняется на величину DL, определяемую соотношением 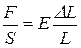 , где постоянная E - модуль Юнга. Ее значение для меди равно E=1,28×1011Н/м2. Используя эту формулу, оцените коэффициент квазиупругой связи между двумя молекулами меди в кристалле.
, где постоянная E - модуль Юнга. Ее значение для меди равно E=1,28×1011Н/м2. Используя эту формулу, оцените коэффициент квазиупругой связи между двумя молекулами меди в кристалле.
в) Рассмотрите бесконечную цепочку атомов меди. Полагая, что коэффициент квазиупругой связи между атомами тот же, что и найденный в пункте (б), найдите верхнюю границу частот упругих волн в цепочке.
г) В состоянии теплового равновесия средняя потенциальная энергия осциллятора равна средней кинетической энергии. Предположим, что при комнатной температуре атомы меди совершают малые колебания около положения равновесия. Оцените в этом предположении потенциальную энергию атома. Используйте полученный результат для оценки среднеквадратичного смещения атома меди от положения равновесия при Т=300°К. Сравните полученное значение со средним расстоянием между атомами. На графике зависимости U(r) проведите уровень средней тепловой энергии атома E=kБ×T.
Задача 6. Температура плавления меди Тпл=1358°К. Оцените размах колебаний атома меди при этой температуре в приближении малых колебаний. Завышено или занижено значение среднеквадратичного отклонения атома при такой оценке?
Задача 7. Используя табличные значения для плотности, модуля Юнга, молярной массы, определите равновесное расстояние между атомами железа и коэффициент жесткости квазиупругой связи между атомами, среднеквадратичное отклонение атомов железа от положений равновесия при Т=300°К.

 , где a и b – коэффициенты, определяемые из эксперимента.
, где a и b – коэффициенты, определяемые из эксперимента. 
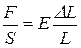 , где постоянная E - модуль Юнга. Ее значение для меди равно E=1,28×1011Н/м2. Используя эту формулу, оцените коэффициент квазиупругой связи между двумя молекулами меди в кристалле.
, где постоянная E - модуль Юнга. Ее значение для меди равно E=1,28×1011Н/м2. Используя эту формулу, оцените коэффициент квазиупругой связи между двумя молекулами меди в кристалле. 


