Работа 18. Проверка уравнения Менделеева-Клапейрона
Лабораторный практикум по физике
1. ЦЕЛЬ РАБОТЫ Целью данной лабораторной работы является экспериментальная проверка уравнения Менделеева-Клапейрона и измерение универсальной газовой постоянной. 2. КРАТКАЯ ТЕОРИЯ Состояние газа можно описывать количественно двумя способами. Один из них – более подробный, он называется микроскопическим. Состояние при этом тоже называется микроскопическим или микросостоянием. Второй способ – менее подробный, он называется макроскопическим, а состояние при этом называется макросостоянием. 2.1. Микросостояние. Газ состоит из молекул, поэтому его состояние определяется тем, в каком состоянии находится каждая из молекул газа. Для описания состояния отдельной молекулы надо выбрать модель молекулы. Простейшая модель – это материальная точка, то есть объект, не имеющий формы и размеров и занимающий в пространстве одну точку. При этом материальная точка обладает массой и может перемещаться в пространстве. Один их постулатов механики утверждает, что состояние материальной точки полностью и однозначно описывается двумя векторами: радиус-вектором r и скоростью 𝑣;. В декартовой системе координат каждому из этих векторов взаимно однозначно сопоставляется тройка чисел, называемых проекциями (координатами) вектора: Микросостояние = или набор 6 N чисел: Микросостояние =
Измерить микросостояние газа или приготовить какое-либо конкретное микросостояние технически невозможно, поэтому с практической точки зрения понятие микросостояния является бесполезным. Однако с теоретической точки зрения исследование микросостояний газа имеет большой интерес. Так как микросостояние с течением времени изменяется сложным, запутанным образом, то используется модель газа, в которой его микросостояние считается случайным. Поэтому для описания поведения газа используется теория вероятностей. Раздел физики, изучающий свойства микросостояний систем, которые состоят из большого числа частиц, называется статистической физикой. 2.2. Макросостояние. Главным свойством макросостояния газа является то, что его можно, во-первых, измерить, а во-вторых, газ можно приготовить в любом из возможных макросостояний. Это означает, что количественно макросостояние описывается небольшим количеством физических величин, которые можно измерять известными в физике приборами. Указанные физические величины называются функциями состояния. Перечислим основные функции состояния. · Объём газа V. Он задаётся сосудом (резервуаром), в котором находится газ. Если сосуда нет, то газ самопроизвольно расширяется, и его объём при этом не имеет какого-то определённого значения. Единица измерения объёма в СИ – м3, наиболее употребительные единицы других систем – см3, мм3, л = дм3. · Температура газа T. Это – степень нагретости газа. Точнее говоря, температура характеризует среднюю кинетическую энергию молекул газа, и задаёт её газу тоже резервуар, а точнее – окружающая среда. Единица измерения температуры в СИ – К, наиболее употребительные единицы других систем – градусы Цельсия, градусы Фаренгейта, градусы Реомюра. · Давление газа p. Это – нормальная[1] составляющая средней силы, которая действует со стороны газа на каждую единицу площади поверхности сосуда или любого предмета, находящегося в газе. Единица измерения давления в СИ – Па, наиболее употребительные единицы других систем – бар, атм, Тор, · Масса газа m. Единица измерения в СИ – кг, наиболее употребительные единицы других систем – г, мг, мкг, Т. · Молярная масса газа m. Эта функция является характеристикой химического состава газа. Её физический смысл – масса одного моля газа. Единица измерения в СИ – кг/моль, наиболее употребительные единицы других систем – г/моль, кг/кмоль. Есть ещё функции состояния: количество молей, плотность газа, концентрация молекул газа, внутренняя энергия, энтропия и др. В данной лабораторной работе они не используются. Из всех функций состояния газа можно выделить минимальный (базовый) набор, обладающий двумя важными свойствами: · во-первых, функции состояния, входящие в базовый набор (базовые функции), не зависят друг от друга, · во-вторых, все остальные функции состояния зависят от базовых функций. Эти свойства базового набора означают, что он полностью и однозначно задаёт макросостояние газа. С математической точки зрения, базовый набор можно собрать не единственным способом, но с точки зрения физики, базовым набором наиболее естественно считать V, T, m и m. Таким образом, Макросостояние = Есть большой класс процессов, в которых масса газа и его химический состав (а значит, и молярная масса) не изменяются. В этом случае m и m не считаются функциями состояния, а считаются неизменными свойствами газа (их называют параметрами). Тогда базовый набор содержит только две функции состояния. Если эти функции состояния понимать как координаты точки на плоскости (её называют фазовой плоскостью), то появляется удобный и наглядный способ изображения макросостояния – в виде точки (фазовой точки) на плоскости. Так как любой процесс, происходящий с газом, есть некоторая упорядоченная смена состояний, то наглядным образом процесса на фазовой плоскости является линия.
|


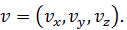 Таким, образом, количественно микросостояние газа, состоящего из N молекул, – это набор 2 N векторов:
Таким, образом, количественно микросостояние газа, состоящего из N молекул, – это набор 2 N векторов: (2.1)
(2.1)
 . 2.2)
. 2.2) .
. . (2.3)
. (2.3)


