Работа Б-1. Определение коэффициента внутреннего трения жидкости по методу Стокса
Цель работы Определить коэффициент внутреннего трения (вязкость) жидкости по методу Стокса. 1. Приборы и принадлежности: 1. Стеклянный цилиндр с исследуемой жидкостью. 2. Масштабная линейка. 3. Секундомер. 4. Металлические шарики. 5. Микрометр. 2. Краткая теория. Вязкость, или внутреннее трение – это явление возникновения силы трения между слоями жидкости или газа, перемещающимися параллельно друг другу с разными по величине скоростями. Чтобы понять происхождение силы внутреннего трения, рассмотрим два соприкасающихся слоя жидкости (газа) А и В некоторой малой толщины dz каждый (рис.1). Слои движутся в одну сторону с различными по величине скоростями
Коэффициент пропорциональности Выражение (1) перепишем как
которое называется эмпирическим уравнением вязкости или уравнением Ньютона. Величина Согласно второму закону Ньютона
Коэффициент вязкости
Из последнего выражения (4) следует физический смысл коэффициента вязкости В формулах (3) и (4) знак «минус» перед правой частью нельзя писать, так как сила трения Исходя из молекулярно–кинетической теории газов коэффициент вязкости
где Из формул (4) и (5) определяется единица измерения в СИ коэффициента вязкости:
3. Описание установки и методика измерения. Лабораторная установка состоит из стеклянного цилиндра, наполненного исследуемой жидкостью. Метод Стокса по определению коэффициента вязкости жидкости состоит в измерении скорости падения шарика в жидкости. Путь, проходимый шариком, измеряют миллиметровой линейкой, наклеенной на цилиндр, а время падения – секундомером. При падении шарика в жидкости к нему прилипает слой жидкости, движущийся вместе с ним. Следующие слои движутся с меньшей скоростью, и эта скорость по модулю будет тем меньше, чем дальше находится слой от движущегося шарика. Между этими слоями вдоль их поверхности и возникает сила трения. Стокс определил силу трения, действующую на шары, при сравнительно небольших скоростях его движения:
где Рассмотрим силы, действующие на шарик, падающий вертикально в жидкости (рис.2).
2. Выталкивающая сила (сила Архимеда), направленная вертикально вверх.
3. Сила трения Сила тяжести
откуда следует, что
Подставляя скорость равномерного движения
где 4. Выполнение работы. 1. Измерить микрометром диаметр шарика. Измерения для каждого шарика проделать несколько раз (не менее трех) в разных положениях. Найти среднее значение радиуса 2. Опустить шарик в цилиндр с исследуемой жидкостью так, чтобы он падал посередине сосуда. С помощью секундомера измерить время 3. Измерить путь 4. Аналогичные измерения проделать с другими шариками. 5. По формуле (7) вычислить коэффициенты вязкости 6. Найти для каждого опыта по среднему значению абсолютную погрешность 7. Результаты измерений и вычислений занести в таблицу. 8.Записать выводы и результат в виде: Таблица измерений и вычислений
5. Контрольные вопросы 1. Какие явления относятся к явлениям переноса? Почему они объединены одним названием? 2. Что называется вязкостью? 3. Как возникают силы внутреннего трения и как они направлены? 4. Каков физический смысл коэффициента вязкости и единица его измерения в СИ? 5. Записать коэффициент вязкости через микроскопические характеристики и по этой формуле проверить его единицу измерения в СИ. 6. В чем состоит метод Стокса по определению вязкости жидкости? 7. Во сколько раз будут отличаться скорости равномерного падения двух шариков из одного материала, у которых радиусы отличаются вдвое
|

 и
и  (пусть
(пусть 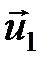 >
>  ). Каждая молекула жидкости участвует в двух движениях: хаотическом, средняя скорость которого
). Каждая молекула жидкости участвует в двух движениях: хаотическом, средняя скорость которого  , и направленном движении со скоростью
, и направленном движении со скоростью  , которая по величине намного меньше, чем
, которая по величине намного меньше, чем  . За счет хаотического движения молекулы из слоя в слой переносят разные импульсы:
. За счет хаотического движения молекулы из слоя в слой переносят разные импульсы:  из слоя А в слой В,
из слоя А в слой В,  из слоя В в слой А. Если
из слоя В в слой А. Если  >
>  , то слой А замедляется, а слой В ускоряется, и через некоторое время направленные скорости слоев выравниваются. Таким образом явление вязкости относится к явлениям переноса и также, как и диффузия и теплопроводность, обусловлено молекулярным механизмом – хаотическим движением и перемешиванием молекул. В явлении вязкости между слоями жидкости возникают силы внутреннего трения, направленные по касательной к поверхности слоев. Направление, в котором отсчитывается расстояние между слоями
, то слой А замедляется, а слой В ускоряется, и через некоторое время направленные скорости слоев выравниваются. Таким образом явление вязкости относится к явлениям переноса и также, как и диффузия и теплопроводность, обусловлено молекулярным механизмом – хаотическим движением и перемешиванием молекул. В явлении вязкости между слоями жидкости возникают силы внутреннего трения, направленные по касательной к поверхности слоев. Направление, в котором отсчитывается расстояние между слоями  (ось
(ось 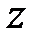 ), перпендикулярно скорости движения слоев. В этом же направлении изменяется и величина скорости
), перпендикулярно скорости движения слоев. В этом же направлении изменяется и величина скорости  .
. Импульс
Импульс 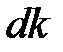 , переданный одному слою другим, тем больший, чем больше выбрана площадь
, переданный одному слою другим, тем больший, чем больше выбрана площадь  переноса импульса соприкасающихся слоев, время
переноса импульса соприкасающихся слоев, время  переноса импульса и изменение величины скорости
переноса импульса и изменение величины скорости  между слоями, то есть, чем больше
между слоями, то есть, чем больше  :
: . (1)
. (1) называют коэффициентом внутреннего трения или коэффициентом вязкости, или просто динамическая вязкость жидкости (газа). Знак «минус» указывает, что импульс переносится в направлении слоя с меньшей скоростью.
называют коэффициентом внутреннего трения или коэффициентом вязкости, или просто динамическая вязкость жидкости (газа). Знак «минус» указывает, что импульс переносится в направлении слоя с меньшей скоростью.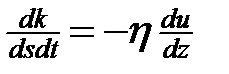 , (2)
, (2) называется плотностью потока импульса и показывает величину импульса переносимого из одного слоя в другой за единицу времени через единичную площадку перпендикулярно этой площадке.
называется плотностью потока импульса и показывает величину импульса переносимого из одного слоя в другой за единицу времени через единичную площадку перпендикулярно этой площадке. , в данном случае
, в данном случае 
 - сила трения между слоями жидкости (газа). Тогда уравнение (2) перепишется
- сила трения между слоями жидкости (газа). Тогда уравнение (2) перепишется . (3)
. (3) . (4)
. (4) : коэффициент вязкости численно равен силе трения, возникающей между двумя слоями жидкости (газа) вдоль поверхности их соприкосновения на единицу площади (
: коэффициент вязкости численно равен силе трения, возникающей между двумя слоями жидкости (газа) вдоль поверхности их соприкосновения на единицу площади ( ) при градиенте величины скорости направленного движения слоев равном единице (
) при градиенте величины скорости направленного движения слоев равном единице ( ).
). представляет одинаковый модуль двух противоположно направленных сил, с которыми слои действуют друг на друга согласно третьему закону Ньютона.
представляет одинаковый модуль двух противоположно направленных сил, с которыми слои действуют друг на друга согласно третьему закону Ньютона. (5)
(5) - средняя длина свободного пробега молекул,
- средняя длина свободного пробега молекул,  - средняя скорость теплового (хаотического) движения молекул,
- средняя скорость теплового (хаотического) движения молекул,  - плотность газа.
- плотность газа. (паскаль-секунда).
(паскаль-секунда). , (6)
, (6)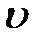 - скорость движения шарика,
- скорость движения шарика,  - радиус шарика,
- радиус шарика,  - коэффициент вязкости жидкости.
- коэффициент вязкости жидкости. 1. Сила тяжести
1. Сила тяжести  , направленная вертикально вниз; масса шарика
, направленная вертикально вниз; масса шарика  (
( – плотность вещества шарика,
– плотность вещества шарика,  – радиус шарика);
– радиус шарика); 
 ,
, 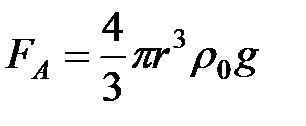 , где
, где 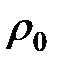 – плотность жидкости.
– плотность жидкости.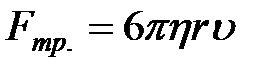 , направленная в сторону, противоположную направлению движения, то есть вертикально вверх.
, направленная в сторону, противоположную направлению движения, то есть вертикально вверх. и сила Архимеда
и сила Архимеда  не зависят от скорости движения шарика, а сила трения
не зависят от скорости движения шарика, а сила трения 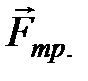 возрастает с увеличением скорости. В начале, когда
возрастает с увеличением скорости. В начале, когда 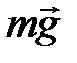 >
>  , шарик движется с ускорением, увеличивая скорость, а, следовательно, и увеличивается
, шарик движется с ускорением, увеличивая скорость, а, следовательно, и увеличивается  . По достижении некоторой определенной скорости, сила трения и выталкивающая сила в сумме уравновешивают силу тяжести и с этого момента шарик начнет двигаться равномерно, то есть с постоянной скоростью
. По достижении некоторой определенной скорости, сила трения и выталкивающая сила в сумме уравновешивают силу тяжести и с этого момента шарик начнет двигаться равномерно, то есть с постоянной скоростью 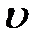
 ,
, .
. , получим формулу:
, получим формулу: , (7)
, (7) – путь,
– путь,  – время равномерного движения шарика в жидкости.
– время равномерного движения шарика в жидкости. шарика.
шарика. падения шарика, начиная с расстояния 3 – 5 см от поверхности жидкости и до дна сосуда. Сначала падение шарика в жидкости ускоренное, а, начиная с глубины 3 – 5 см, становится равномерным. Время
падения шарика, начиная с расстояния 3 – 5 см от поверхности жидкости и до дна сосуда. Сначала падение шарика в жидкости ускоренное, а, начиная с глубины 3 – 5 см, становится равномерным. Время 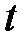 записать в таблицу.
записать в таблицу. , пройденный шариком при равномерном движении в жидкости.
, пройденный шариком при равномерном движении в жидкости.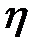 для каждого опыта. Определить среднее значение
для каждого опыта. Определить среднее значение  .
. , а затем среднее значение
, а затем среднее значение 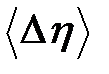 .
. .
. = 11300
= 11300  ,
,  1260
1260 




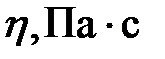



 )?
)?


