Краткая теория
Коэффициент Пуассона g – это параметр адиабатного процесса. Он входит в известное уравнение Пуассона, описывающее адиабатный процесс в идеальном газе. Рассмотрим, что это за уравнение и как оно выводится. Адиабатным называется процесс, протекающий без теплообмена с окружающей средой, На практике он может быть осуществлен в системе, окруженной теплоизоляционной оболочкой, но поскольку для теплообмена необходимо некоторое время, то адиабатным можно считать также процесс, который протекает так быстро, что система не успевает вступить в теплообмен с окружающей средой. Для получения уравнения адиабатного процесса удобно начать с первого закона термодинамики. Согласно первому закону термодинамики количество теплоты
Увеличение внутренней энергии идеального газа в случае изменения его температуры на
Здесь i – число степеней свободы молекулы, под которым подразумевается число независимых координат, определяющих положение молекулы в пространстве: i = 3 для одноатомной молекулы, i = 5 – для двухатомной, i = 6 – для многоатомной, R – универсальная газовая постоянная, Работа газа определяется выражением:
Для адиабатного процесса из формул (3.1) – (3.3) следует:
Это – дифференциальное уравнение, связывающее два дифференциала dT и dV. Но в нём присутствуют не функции T и V, а функция P. Поэтому надо либо функцию P выразить через T и V, либо один из дифференциалов dT или dV выразить через дифференциал dP. Последнее можно сделать, продифференцировав уравнение Клапейрона – Менделеева.
Подставив (3.5) в (3.4), получим:
Решение этого дифференциального уравнения можно получить методом разделения переменных. Для этого разделим обе части уравнения на PV.
Проинтегрировав левую и правую часть получаем:
Потенцирование этого уравнения даёт:
Последнее уравнение и есть упоминавшееся выше уравнение Пуассона. Для краткости в нём показатель степени
Интересно, что коэффициент Пуассона можно выразить через теплоёмкости газа при постоянном давлении и при постоянном объёме. Отметим сначала, что физическая величина «теплоёмкость» бывает трёх типов: полная, удельная и молярная. Полная теплоёмкость C есть величина, равная количеству теплоты, которое необходимо сообщить данной системе для увеличения её температуры на один градус. Это значит, что
Удельной теплоёмкостью вещества называется величина c, равная теплоёмкости единице массы этого вещества.
Теплоёмкость одного моля вещества называется молярной теплоемкостью:
где n – количество молей. Если газ нагревать при постоянном объёме, то
Если газ нагревать при постоянном давлении, то полученное газом количество теплоты расходуется на увеличение внутренней энергии dU и выполнение работы
Тогда молярная теплоёмкость идеального газа при постоянном давлении равна:
Используя уравнение Клапейрона – Менделеева, можно доказать, что
Поэтому из (3.10) и (3.11) следует, во-первых, уравнение Майера
а во-вторых,
Поделив (3.13) на (3.10), получим интересный результат:
|

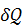 =0.
=0.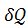 , сообщённое системе, расходуется на увеличение внутренней энергии dU и на выполнение системой работы
, сообщённое системе, расходуется на увеличение внутренней энергии dU и на выполнение системой работы  :
: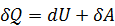 . (3.1)
. (3.1) равно:
равно: . (3.2)
. (3.2) .
. . (3.3)
. (3.3) . (3.4)
. (3.4) . (3.5)
. (3.5)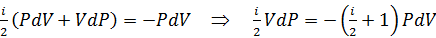 .
. .
. .
.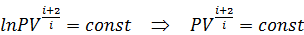 .
. обозначают одной буквой g и называют показателем адиабаты или коэффициентом Пуассона. Итак, уравнение Пуассона имеет вид:
обозначают одной буквой g и называют показателем адиабаты или коэффициентом Пуассона. Итак, уравнение Пуассона имеет вид: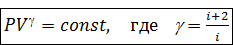 . (3.6)
. (3.6) . (3.7)
. (3.7) . (3.8)
. (3.8) , (3.9)
, (3.9)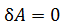 и согласно (3.1) всё полученное газом количество теплоты расходуется только на увеличение его внутренней энергии
и согласно (3.1) всё полученное газом количество теплоты расходуется только на увеличение его внутренней энергии 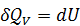 . Тогда из (3.7) и (3.2) следует, что молярная теплоёмкость идеального газа при постоянном объёме равна:
. Тогда из (3.7) и (3.2) следует, что молярная теплоёмкость идеального газа при постоянном объёме равна: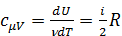 . (3.10)
. (3.10)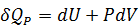 .
.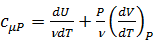 . (3.11)
. (3.11) .
.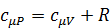 , (3.12)
, (3.12)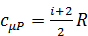 . (3.13)
. (3.13) . (3.14)
. (3.14)


