Уравнение Менделеева-Клапейрона
Связь функций состояния газа с базовыми функциями зависит от того, какая используется модель газа. Простейшей моделью является идеальный газ. Он представляет собой множество не взаимодействующих друг с другом молекул. Моделью молекулы при этом может быть материальная точка (атом) или несколько связанных друг с другом атомов. Формулы, определяющие связь функций состояния газа с базовыми функциями, называются уравнениями состояния. Одним из наиболее известных уравнений состояния идеального газа является уравнение Менделеева-Клапейрона, которое связывает давлениегаза p с V, T, m и m:
Буквой R обозначена константа, называемая универсальной газовой постоянной. В предлагаемой лабораторной работе необходимо экспериментально проверить это уравнение. 3. МЕТОДИКА ЭКСПЕРИМЕНТА Полная комплексная проверка уравнения Менделеева-Клапейрона означает экспериментальное исследование четырёх зависимостей: Исследуемый газ – воздух в стеклянной колбе. Сначала колба открыта и заполнена атмосферным воздухом. Затем из колбы выкачивается воздух, что приводит к уменьшению массы воздуха в колбе m и его давления p. Если в процессе выкачивания воздуха измерять m и p, то можно получить зависимость p (m). Вопрос только в том, как измерять m и p. Измерение давления воздуха в колбе p. Типовой манометр или вакуумметр, присоединённые к колбе, измеряют на самом деле не p, а разницу p ' между давлением воздуха в колбе и давлением атмосферного воздуха
Измерение массы воздуха в колбе m. Если с помощью весов измерить массу колбы с воздухом m ' и каким-то образом отдельно измерить массу колбы без воздуха
Интересно, что для экспериментальной проверки уравнения Менделеева-Клапейрона не обязательно измерять атмосферное давление
Формула (3.3) означает, что при условии правильности уравнения Менделеева-Клапейрона показание вакуумметра p ' зависит от показания весов m ' линейно. Параметры этой линейной зависимости, то есть свободный член C и угловой коэффициент k, определяются формулами (3.5). Таким образом, для проверки уравнения Менделеева-Клапейрона надо получить экспериментальную зависимость p '(m '), построить график этой зависимости и убедиться, что этот график представляет собой прямую линию[2]. Если зависимость p '(m ') действительно окажется линейной, то из второй формулы в (3.4) следует, что проведённый эксперимент позволяет получить дополнительную информацию: измерить универсальную газовую постоянную R. Для этого надо измерить угловой коэффициент k зависимости p '(m '), температуру воздуха T, объём колбы V, а затем узнать значение R по формуле
Примечание. В ходе экспериментов воздух из колбы выкачивается, поэтому 4. ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
Лабораторная работа выполняется на установке настольного типа ФПТ1-12, изготовленной в НПП «Учебная техника», г. Ровно. Фотография установки показана на рисунке 4.1. Установка состоит из следующих элементов. · Измерительный блок. В его состав входят: а) компрессор, выкачивающий воздух из стеклянной колбы, которая соединена с компрессором гибкой трубкой, б) вакуумметр, показывающий разность p ' между давлением воздуха в колбе и атмосферным давлением, в) термометр, показывающий температуру атмосферного воздуха T. · Стеклянная колба, содержащая исследуемый газ. В данной работе газ – это атмосферный воздух. · Электронные цифровые весы для измерения массы колбы с воздухом m '. 5. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 5.1. Включите в сеть шнуры питания электронных весов и измерительного блока. 5.2. Включите тумблером «СЕТЬ» измерительный блок. При этом должна загореться индикаторная лампочка. 5.3. Посмотрите на приборы измерительного блока. Стрелка вакуумметра должна стоять на отметке 0. Если это не так, обратитесь к преподавателю или лаборанту. 5.4. Запишите в таблицу 5.1 температуру воздуха, показания весов m ' и вакуумметра p '. 5.5. Включите компрессор кнопкой «ПУСК» и несколько секунд не отпускайте эту кнопку. Когда стрелка вакуумметра передвинется на 2-4 малых деления, отпустите кнопку «ПУСК», подождите примерно 5 секунд и запишите в таблицу 5.1 показания весов m ' и вакуумметра p '. При записи показаний вакуумметра знак «минус» не учитывайте [3]. 5.6. Повторите пункт 5.5 ещё 5 раз. Таблица 5.1. Зависимость показаний вакуумметра p '
5.7. Выключить тумблером «СЕТЬ» измерительный блок. При этом индикаторная лампочка должна погаснуть. 5.8. На основании данных таблицы 5.1 постройте график экспериментальной зависимости p '(m '). · Выделите для графика не менее половины страницы. · Выберите подходящий масштаб, имея в виду, что по горизонтальной оси (оси абсцисс) надо откладывать значения m ', а по вертикальной оси (оси ординат) – значения p '. · Нанесите на график экспериментальные точки в виде не закрашенных кружочков диаметром примерно 2 мм. · Нанесите на график планки погрешностей. Это значит, что надо от каждой экспериментальной точки отложить влево и вправо отрезок длиной D(m '), а затем отложить вверх и вниз отрезок длиной D(p '). Как оценить погрешности D(m ') и D(p '), написано в пункте 6. · Проведите по линейке экспериментальную прямую – так, чтобы она пересекла планки погрешностей всех экспериментальных точек и при этом прошла наиболее близко ко всем точкам. Образец показан на рисунке 5.1. 5.9. Для этого выберите на экспериментальной прямой две произвольные точки 1 и 2, отметьте их и определите их координаты
Например, на рисунке 5.1 выбрана точка 1 с координатами (100,48 г; 0,6 бар). Точка 2 выбрана на оси абсцисс, но не показана, так как она находится совсем рядом с экспериментальной точкой. Координаты точки 2: (101,21 г; 0 бар). При этом получается:
Графики можно строить, используя современные компьютерные программы. Например, график на рисунке 5.1 построен с помощью EXCEL. Программа сама провела по точкам экспериментальную линию (линию тренда) и выдала её уравнение: y = –0,8321 x + 84,21. Из этого уравнения видно, что 5.10. Определите, используя формулу (3.5), экспериментальное значение универсальной газовой постоянной R и оцените погрешность измерения D(R). О том, как оценивать погрешности измерений в данной лабораторной работе, написано в пункте 6. 5.11. Запишите результат измерения универсальной газовой постоянной в виде:
5.12. Сформулируйте выводы. 6. ОЦЕНКА ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ 6.1. Погрешности прямых измерений. В данной лабораторной работе прямым способом измеряются три величины: разность давлений p ', масса колбы с воздухом m ' и температура воздуха T. Разность p ' между давлением воздуха в колбе p и атмосферным давлением p 0 измеряется вакуумметром. Это – стрелочный прибор с классом точности 0,05 b, что означает: D(p ') = 0,05 бар. Масса колбы с воздухом m ' измеряется электронными весами, которые являются цифровым прибором с классом точности 0,01 г. Это означает, что D(m ') = 0,01 г. Температура воздуха T измеряется цифровым термометром с классом точности 1°С, так что D(T) = 1 К. 6.2. Погрешности заданных величин. В данном методическом пособии (в таблице 5.1) указано: объём колбы V = 1,0 л, молярная масса воздуха 6.3. Погрешность измерения углового коэффициента k линейной зависимости p '(m '). Согласно [8.4], эту погрешность можно оценить так. · Проведите на графике зависимости p '(m ') две вспомогательные прямые линии (временно). Обе они должны пройти через планки погрешностей экспериментальных точек, но при этом первую из вспомогательных линий надо провести как можно круче, а вторую – как можно более полого. · Измерьте описанным в пункте 5.9 методом два предельных значения углового коэффициента, используя сначала первую вспомогательную прямую, затем – вторую. Это будет k max и k min. · Определите погрешность D(k) по формуле:
· Удалите с графика вспомогательные прямые линии. 6.4. Погрешность измерения универсальной газовой постоянной R. Эта величина измеряется косвенно, с использованием формулы (3.5). Из формулы следует, что
7. КОНТРОЛЬНЫЕ ВОПРОСЫ 7.1. В чём отличие между микросостоянием и макросостоянием? 7.2. Какие функции состояния газа вы знаете? 7.3. Какие функции состояния газа являются базовыми? 7.4. Что такое уравнения состояния? 7.5. Какие уравнения состояния идеального газа вы знаете? 7.6. Насколько полной является проверка уравнения Менделеева-Клапейрона в данной лабораторной работе? 7.7. Какие результаты данной лабораторной работы свидетельствуют о правильности уравнения Менделеева-Клапейрона? 7.8. Что показывает вакуумметр, используемый в данной лабораторной работе? 7.9. Что измеряется в данной лабораторной работе с помощью электронных весов? 7.10. В чём состоит способ измерения универсальной газовой постоянной, применяемый в данной лабораторной работе?
|

 . (2.4)
. (2.4)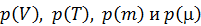 . В данной работе предлагается исследовать только одну из этих зависимостей – p (m) при неизменных значениях V, T, m.
. В данной работе предлагается исследовать только одну из этих зависимостей – p (m) при неизменных значениях V, T, m. . Следовательно, величину p можно измерить косвенно, на основе прямых измерений p ' и
. Следовательно, величину p можно измерить косвенно, на основе прямых измерений p ' и  и формулы
и формулы . (3.1)
. (3.1) , то массу воздуха в колбе можно измерить косвенно, на основе прямых измерений m ' и
, то массу воздуха в колбе можно измерить косвенно, на основе прямых измерений m ' и  . (3.2)
. (3.2) , (3.3)
, (3.3) . (3.4)
. (3.4) . (3.5)
. (3.5) и показания вакуумметра – отрицательные. Удобнее пользоваться положительными числами, то есть вместо p ' использовать
и показания вакуумметра – отрицательные. Удобнее пользоваться положительными числами, то есть вместо p ' использовать  . Тогда при снятии показаний вакуумметра знак «минус» учитывать не надо. Для того, чтобы не усложнять обозначения, удобно знак модуля не писать и обозначение p ' понимать как
. Тогда при снятии показаний вакуумметра знак «минус» учитывать не надо. Для того, чтобы не усложнять обозначения, удобно знак модуля не писать и обозначение p ' понимать как 
 ,
T =
,
T =

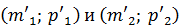 . После этого угловой коэффициент можно определить по формуле
. После этого угловой коэффициент можно определить по формуле . (5.1)
. (5.1)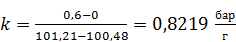 .
.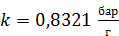 . Данное значение углового коэффициента точнее, чем вышеуказанное число
. Данное значение углового коэффициента точнее, чем вышеуказанное число  .
. .
.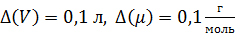 .
. . (6.1)
. (6.1) . (6.2)
. (6.2)


