Метод измерения коэффициента Пуассона
Метод определения показателя адиабаты (коэффициета Пуассона), предложенный Клеманом и Дезормом (1819 г.), основывается на изучении параметров некоторой массы газа, переходящей из одного состояния в другое двумя последовательными процессами - адиабатным и изохорным. Эти процессы на диаграмме P-V (рис. 3.1) изображены кривыми соответственно 1-2 и 2-3. Если в сосуд, соединенный с дифференциальным датчиком давления, накачать воздух и подождать до установления теплового равновесия с окружающей средой, то в этом начальном состоянии 1 газ имеет параметры P 1, V 1, T 1, причем температура газа в сосуде равна температуре окружающей среды T 1 = T 0, а давление Р 1= Р 0 + P ¢ немного больше атмосферного. Если теперь на короткое время соединить сосуд с атмосферой, то произойдет адиабатное расширение воздуха. При этом воздух в сосуде перейдет в состояние 2, его давление понизится до атмосферного P 2 = P 0. Масса воздуха, оставшегося в сосуде, которая в состоянии 1 занимала часть объема сосуда, расширяясь, займет весь объем V 2. При этом температура воздуха, оставшегося в сосуде, понизится до T 2.
Поскольку процесс 1-2 – адиабатный, к нему можно применить уравнение Пуассона (3.6):
Отсюда
После кратковременного соединения сосуда с атмосферой охлажденный из-за адиабатного расширения воздух в сосуде будет нагреваться (процесс 2-3) до температуры окружающей среды Поскольку процесс 2-3 – изохорный, к нему можно применить закон Шарля:
Отсюда
Из уравнений (4.12) и (4.2) получим:
Прологарифмируем левую и правую части этого уравнения:
Избыточные давления Р¢ и Р¢¢ очень малы по сравнению с атмосферным давлением Р0, поэтому можно применить приближённое равенство
Из (4.4) получается рабочая формула для определения коэффициента Пуассона
Избыточные давления Р' и Р" измеряют с помощью манометра.
|

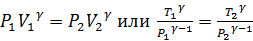 . (4.1)
. (4.1)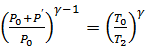 .
. при постоянном объёме
при постоянном объёме  . При этом давление в сосуде поднимется до
. При этом давление в сосуде поднимется до  .
. .
. . (4.2)
. (4.2) .
. . (4.3)
. (4.3) . (4.4)
. (4.4) :
: . (4.5)
. (4.5)


