Формула Стокса
Закон Ньютона для внутреннего трения позволяет решить многие задачи, связанные с движением жидкости и газа, а также с движением твёрдых тел в жидкой и в газообразной среде. Эти задачи и методы их решения подробно рассмотрены в курсах гидродинамики и аэродинамики. Задача данной лабораторной работы – исследование характера движения твёрдого шарика, брошенного в жидкость. Чтобы решить эту задачу, надо знать какие силы действуют на шарик при его падении и как вычислить эти силы. Одна из этих сил – сила сопротивления F с, действующая на шарик против его скорости со стороны обтекающего шарик слоя жидкости. Итак, найдём формулу для этой силы, опираясь на закон Ньютона для внутреннего трения. Сила F с направлена вертикально вверх и складывается она из вертикальных проекций сил внутреннего трения d F, действующих со стороны жидкости на каждый элемент поверхности шарика dS – см. рисунок 3.1. Величина dF определяется формулой (3.6), поэтому
 , а скорость жидкости по мере удаления от поверхности шарика изменяется от 𝑣 до 0, то для каждой точки можно подобрать такое число L, что , а скорость жидкости по мере удаления от поверхности шарика изменяется от 𝑣 до 0, то для каждой точки можно подобрать такое число L, что
где L – некоторая величина, имеющая размерность длины. Эта величина примерно равна толщине слоя жидкости, который увлекает движущийся шарик. Естественно, что на градиент скорости, а значит, и на величину L влияют форма и размеры сосуда, в котором находится жидкость. Учёт влияния сосуда усложняет задачу, но, к счастью, это влияние тем меньше, чем дальше от стен сосуда находится шарик. Будем считать, что сосуд достаточно велик и его влияние на движение шарика незначительно. При подстановке (3.10) в (3.9) скорость шарика тоже можно вынести из-под интеграла, так что
Интеграл в (3.11) зависит только от размеров шарика. Вычисление его – задача, выходящая за рамки общей физики. Один из основателей гидродинамики Дж.Г. Стокс[10] показал, что этот интеграл равен
Эта формула называется формулой Стокса. Она даёт достаточно точный результат при выполнении следующих двух условий. · В жидкости при падении шарика не возникает турбулентности. Это условие выполняется, если шарик движется не слишком быстро. Для этого надо опускать его в жидкость плавно, без броска, то есть с нулевой начальной скоростью. Кроме того, надо, чтобы плотность вещества, и которого сделан шарик, была не намного больше плотности жидкости – тогда шарик при падении разгоняется до небольшой скорости. · Горизонтальный размер сосуда должен быть как минимум в 5 – 10 раз больше диаметра шарика. В данной лабораторной работе оба условия выполняются. Во-первых, используются достаточно вязкие и плотные жидкости, так что падающие шарики разгоняются всего до 2 – 3 см/c. Во-вторых, диаметр шариков не более 5 мм, а сосуд – это цилиндрический стакан диаметром около 5 см.
|

 . (3.9)
. (3.9) , (3.10)
, (3.10)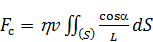 . (3.11)
. (3.11) , где r – радиус шарика. Таким образом,
, где r – радиус шарика. Таким образом, . (3.12)
. (3.12)


