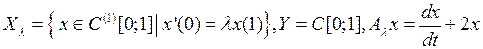 .
.
Решение. Для нахождения обратного оператора рассмотрим в 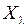 уравнение
уравнение 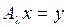 , т. е. линейное дифференциальное уравнение
, т. е. линейное дифференциальное уравнение
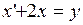 . (7)
. (7)
Нужно выяснить, при каких значениях 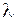 у этого уравнения для любого
у этого уравнения для любого 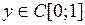 существует единственное решение
существует единственное решение 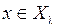 . Другими словами, для любого
. Другими словами, для любого 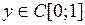 краевая задача
краевая задача
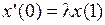 (8)
(8)
для уравнения (7) должна иметь единственное непрерывно дифференцируемое решение. Воспользовавшись формулой для общего решения линейного дифференциального уравнения первого порядка, получим общее решение уравнения (7):
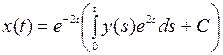 . (9)
. (9)
Требуется узнать, при каких 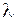 для любого
для любого 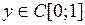 найдется такое С, при котором формула (9) дает решение задачи (8). Подставив (9) в (8), получим после упрощений
найдется такое С, при котором формула (9) дает решение задачи (8). Подставив (9) в (8), получим после упрощений
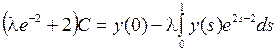 . (10)
. (10)
Возможны два случая.
а) 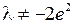 . Тогда уравнение (11) имеет единственное решение
. Тогда уравнение (11) имеет единственное решение
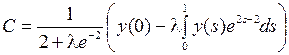
для любого 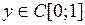 . Следовательно, при этих
. Следовательно, при этих 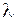 существует обратный оператор, который мы найдем, подставив это значение С в равенство (9):
существует обратный оператор, который мы найдем, подставив это значение С в равенство (9):
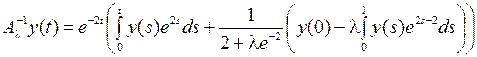 .
.
В силу теоремы Банаха об обратном операторе непрерывность этого оператора будет следовать из непрерывности оператора 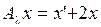 . Последний же факт легко доказать по Гейне. Действительно, если
. Последний же факт легко доказать по Гейне. Действительно, если  в пространстве
в пространстве  , то это значит, что
, то это значит, что  и
и 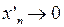 равномерно на
равномерно на  . Но тогда и
. Но тогда и  равномерно на
равномерно на  ;
;
б) 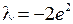 . В этом случае уравнение (10) имеет вид
. В этом случае уравнение (10) имеет вид
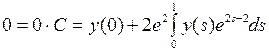 .
.
Но правая часть этого уравнения при некоторых непрерывных у (например, при  ) не будет равна 0. Следовательно, при этих у последнее уравнение не имеет решения (относительно С), а потому оператор
) не будет равна 0. Следовательно, при этих у последнее уравнение не имеет решения (относительно С), а потому оператор 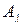 не является сюръективным.
не является сюръективным.
Итак, обратный к оператору 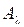 существует тогда и только тогда, когда
существует тогда и только тогда, когда 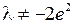 . Причем при таких значениях
. Причем при таких значениях 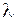 оператор
оператор 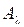 непрерывно обратим.
непрерывно обратим.
Министерство образования Республики Беларусь

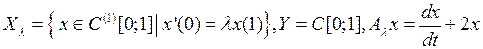 .
.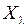 уравнение
уравнение 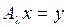 , т. е. линейное дифференциальное уравнение
, т. е. линейное дифференциальное уравнение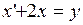 . (7)
. (7)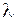 у этого уравнения для любого
у этого уравнения для любого 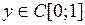 существует единственное решение
существует единственное решение 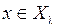 . Другими словами, для любого
. Другими словами, для любого 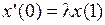 (8)
(8)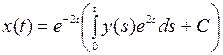 . (9)
. (9)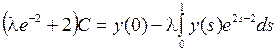 . (10)
. (10)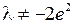 . Тогда уравнение (11) имеет единственное решение
. Тогда уравнение (11) имеет единственное решение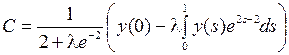
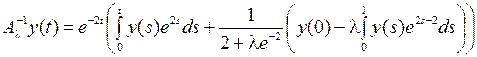 .
.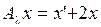 . Последний же факт легко доказать по Гейне. Действительно, если
. Последний же факт легко доказать по Гейне. Действительно, если  в пространстве
в пространстве  , то это значит, что
, то это значит, что 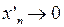 равномерно на
равномерно на  . Но тогда и
. Но тогда и  равномерно на
равномерно на 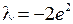 . В этом случае уравнение (10) имеет вид
. В этом случае уравнение (10) имеет вид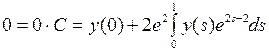 .
. ) не будет равна 0. Следовательно, при этих у последнее уравнение не имеет решения (относительно С), а потому оператор
) не будет равна 0. Следовательно, при этих у последнее уравнение не имеет решения (относительно С), а потому оператор 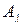 не является сюръективным.
не является сюръективным.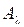 существует тогда и только тогда, когда
существует тогда и только тогда, когда 


