Элементы теории множеств
В «наивной», т. е. не аксиоматической, теории множеств понятия «множество» и «элемент множества» считаются основными и не определяются. Задать множество – это значит указать, из каких элементов оно состоит. Равенство множеств А и В означает, что они состоят из одних и тех же элементов. Для этого достаточно показать, что каждый элемент множества А принадлежит В и обратно, каждый элемент множества В принадлежит А. Если некоторое отображение (функция) f определено на множестве X и принимает значения в множестве Y, то этот факт записывается следующим образом: В этом случае Х называется областью (множеством) определения отображения f, а Y – областью (множеством) прибытия этого отображения. При этом множество значений, которое принимает отображение f на множестве X, называется еще образом множества X при отображении f и обозначается f (Х). Таким образом,
Аналогично определяется образ f (А) любого подмножества А множества Х (дайте это определение). Если
Отметим, что, вообще говоря, Понятие биективного отображения позволяет сравнивать бесконечные множества «по величине». В частности, множества X и Y называют равномощными (эквивалентными), если существует биективное отображение Простейшее из бесконечных множеств – это множество Отметим следующие свойства счетных множеств. Теорема 1. Всякое бесконечное множество A имеет счетное подмножество. Теорема 2. Всякое подмножество счетного множества конечно или счетно. Теорема 3. (основная теорема теории счетных множеств). 1) объединение конечного семейства счетных множеств счетно; 2) объединение счетного семейства счетных множеств счетно; 3) объединение счетного семейства непустых конечных множеств счетно. Следствие 1. Прямое произведение конечного семейства счетных множеств счетно. Следствие 2. Множество рациональных чисел Часто бывает полезной Лемма о сравнении мощностей. Пусть 1) Если 2) Если Важной является следующая теорема: Теорема 4 (Кантор). Множество действительных чисел несчетно. Множества, эквивалентные множеству действительных чисел, называются множествами мощности континуум. Нам потребуются следующие системы множеств, которые часто служат областями определения мер. Определение 1. Пусть 1) 2) Алгебра множеств обладает следующими свойствами: 3) Ø, 4) 5) Таким образом, операции объединения, пересечения и разности, произведенные конечное число раз, не выводят из алгебры множеств. Определение 2. Пусть 1) 2) Легко доказать, что Определение 3. Пусть 1) 2) 3)
1.1.1 Пусть A, B, C, D – произвольные множества. Доказать данные равенства (таблица 1.1.1).
Таблица 1.1.1
1.1.2 Пусть
Таблица 1.1.2
1.1.3 Выяснить, являются ли следующие множества конечными, счетными или множествами мощности континуум.
Вариант 1. Множество всех упорядоченных пар натуральных чисел. Вариант 2. Множество всех конечных последовательностей рациональных чисел длины 3. Вариант 3. Множество всех многочленов с целыми коэффициентами степени не выше 4. Вариант 4. Множество всех прямоугольников на плоскости с вершиной Вариант 5. Множество треугольников на плоскости вершиной Вариант 6. Множество всех открытых кругов на плоскости натурального радиуса, координаты центра которых рациональны. Вариант 7. Множество всех параллелограммов на плоскости вершиной Вариант 8. Множество всех замкнутых кругов на плоскости, у которых координаты центра и площадь являются натуральными числами. Вариант 9. Множество всех кубов в трехмерном пространстве с вершиной Вариант 10. Множество всех шаров в трехмерном пространстве, у которых координаты центра и радиус – натуральные числа. Вариант 11. Множество всех подмножеств множества Вариант 12. Множество всех многочленов с рациональными коэффициентами.
1.1.4 Выяснить, образуют ли полуалгебру, алгебру,
Вариант 1. Всевозможные промежутки вида Вариант 2. Всевозможные дуги единичной окружности Т (как содержащие, так и не содержащие свои концы),включая пустую дугу и всю Т, Х Вариант 3. Всевозможные дуги единичной окружности Т (как содержащие, так и не содержащие свои концы), длина которых меньше числа Вариант 4. Всевозможные промежутки, содержащиеся в отрезке Вариант 5. Всевозможные промежутки, содержащиеся в Вариант 6. Все конечные и счетные подмножества множества Вариант 7. Всевозможные прямоугольники вида Вариант 8. Множество всех прямоугольников на координатной плоскости Вариант 9. Все ограниченные промежутки числовой прямой Вариант 10. Всевозможные промежутки вида Вариант 11. Множество всех конечных подмножеств счетного множества Х. Вариант 12. Множество всех квадрируемых (измеримых по Жордану) фигур на плоскости
|

 .
. .
. , то прообразом множества С при отображении f называется множество всех точек из X, которые отображение f переводит в С. Это множество обозначают
, то прообразом множества С при отображении f называется множество всех точек из X, которые отображение f переводит в С. Это множество обозначают  . Таким образом,
. Таким образом,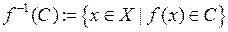 .
. . В случае, если равенство имеет место, отображение f называется сюръективным (разумеется, при фиксированном X это свойство зависит от выбора множества Y). Если отображение f разные точки множества X переводит в разные, оно называется инъективным. Биективным (биекцией) называется отображение, которое инъективно и сюръективно.
. В случае, если равенство имеет место, отображение f называется сюръективным (разумеется, при фиксированном X это свойство зависит от выбора множества Y). Если отображение f разные точки множества X переводит в разные, оно называется инъективным. Биективным (биекцией) называется отображение, которое инъективно и сюръективно. ). Мы пишем
). Мы пишем  и говорим, что мощность множества X не превосходит мощности множества Y, если множество
и говорим, что мощность множества X не превосходит мощности множества Y, если множество  эквивалентно некоторому подмножеству множества
эквивалентно некоторому подмножеству множества  . Это бинарное отношение является отношением порядка.
. Это бинарное отношение является отношением порядка. натуральных чисел. Эквивалентные ему множества называются счетными. Другими словами, множество счетно, если его элементы можно занумеровать натуральными числами, т. е. «расположить в последовательность». Легко видеть, что множество, эквивалентное счетному множеству, само счетно (почему?).
натуральных чисел. Эквивалентные ему множества называются счетными. Другими словами, множество счетно, если его элементы можно занумеровать натуральными числами, т. е. «расположить в последовательность». Легко видеть, что множество, эквивалентное счетному множеству, само счетно (почему?). счетно.
счетно. инъективно, то
инъективно, то 

 – непустое множество. Непустая система
– непустое множество. Непустая система  подмножеств множества
подмножеств множества  ;
; .
. ;
; ;
; .
. подмножеств множества
подмножеств множества  - алгеброй, если она удовлетворяет следующим условиям:
- алгеброй, если она удовлетворяет следующим условиям: .
. .
. подмножеств множества
подмножеств множества  ;
; ;
; .
.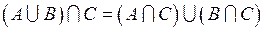






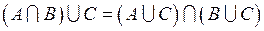




 . Найти и изобразить следующие множества:
. Найти и изобразить следующие множества:  . Выяснить, является ли отображение
. Выяснить, является ли отображение 


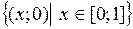



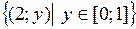
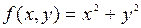


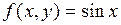
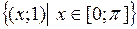















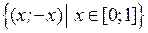

 , у которых координаты вершин рациональны.
, у которых координаты вершин рациональны. , у которых координаты вершин – целые числа.
, у которых координаты вершин – целые числа.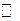 , состоящих из трех элементов.
, состоящих из трех элементов. -алгебру следующие системы подмножеств множества Х.
-алгебру следующие системы подмножеств множества Х.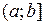 , содержащиеся в полуинтервале
, содержащиеся в полуинтервале  ,
,  .
. Т.
Т.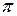 , к которым добавлена пустая дуга и Т, Х
, к которым добавлена пустая дуга и Т, Х  , Х
, Х  .
. , Х
, Х 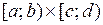 , содержащиеся в квадрате
, содержащиеся в квадрате  , Х
, Х  .
. (как содержащих, так и не содержащих некоторые свои стороны), стороны которых параллельны осям координат, включая пустой прямоугольник и
(как содержащих, так и не содержащих некоторые свои стороны), стороны которых параллельны осям координат, включая пустой прямоугольник и  , содержащиеся в полуинтервале
, содержащиеся в полуинтервале 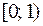 ,
,  ;
;


