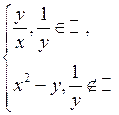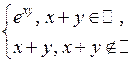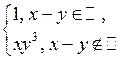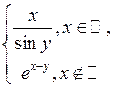Измеримые функции. Интеграл Лебега
Всюду ниже Определение 1. Функция
принадлежит Семейство всех измеримых функций образует алгебру относительно поточечных операций сложения и умножения функций, а также умножения функции на число. Определение 2. Функция Простые функции тоже образуют алгебру относительно поточечных операций сложения и умножения функций, а также умножения функции на число. Важным примером простой функции является индикатор множества
Каждая простая функция единственным образом может быть представлена в виде
где числа Определение 3. Пусть
Интеграл от функции
Определение 4. Пусть f – неотрицательная измеримая функция на
где Возможны и другие (равносильные) определения (см., напр., [2, 6]). Определение 5. Пусть f – измеримая функция на
при условии, что интегралы в правой части существуют и конечны. При этом функция f называется интегрируемой (пишут Интеграл Лебега функции f по множеству
Теорема 1 (о сравнении интеграла Лебега с собственным интегралом Римана). Если функция Аналогичный результат верен и для n -кратного интеграла. Теорема 2 (критерий Лебега интегрируемости по Риману). Функция Теорема 3 Если
1.3.1 Докажите, что функция Таблица 1.3.1
1.3.2 Для функции а) выяснить, является ли б) найти меру Лебега множества ее точек разрыва; в) определить, существует ли от нее собственный или несобственный интеграл Римана; г) выяснить, измерима ли д) найти интеграл Лебега
Таблица 1.3.2
Окончание таблицы 1.3.2
1.3.3 Доказатьсуществование и вычислить
Таблица 1.3.3
|

 есть
есть  -аддитивная мера, определенная на
-аддитивная мера, определенная на  подмножеств множества Х. Элементы системы
подмножеств множества Х. Элементы системы 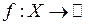 называется
называется 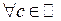 множество
множество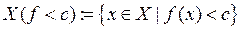
 называется простой, если она измерима и множество ее значений конечно.
называется простой, если она измерима и множество ее значений конечно. (характеристическая функция множества
(характеристическая функция множества  ), определяемый равенством
), определяемый равенством .
.
 попарно различны,
попарно различны,  . Это представление называется каноническим.
. Это представление называется каноническим. – неотрицательная простая функция на
– неотрицательная простая функция на  с каноническим представлением
с каноническим представлением

 ,
,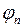 – последовательность неотрицательных простых функций, которая не убывая сходится к f.
– последовательность неотрицательных простых функций, которая не убывая сходится к f. и
и 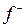 – ее положительная и отрицательная части соответственно. Интеграл от функции f определяется равенством
– ее положительная и отрицательная части соответственно. Интеграл от функции f определяется равенством
 ).
). определяется равенством
определяется равенством .
. интегрируема по Риману, то
интегрируема по Риману, то  и
и 
 -п.в., то
-п.в., то  и
и .
. является простой, а затем, пользуясь определением интеграла от простой функции, вычислите
является простой, а затем, пользуясь определением интеграла от простой функции, вычислите  (таблица 1.3.1).
(таблица 1.3.1).

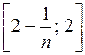
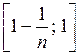


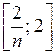
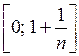




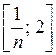
 ограниченной;
ограниченной; , если он существует.
, если он существует.



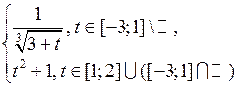








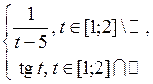

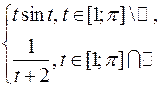

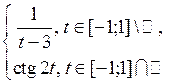



 , где
, где ,
,  плоская мера Лебега (таблица 1.3.3).
плоская мера Лебега (таблица 1.3.3).