1 Пусть  , и
, и 
Вычислить  .
.
Пример 1.  .
.
Решение. Воспользуемся тем, что для любой кусочно-непрерывно-дифференцируемой функции  , имеющей только точки разрыва первого рода
, имеющей только точки разрыва первого рода  со скачками
со скачками  соответственно и непрерывной слева, и для любой функции
соответственно и непрерывной слева, и для любой функции  (здесь и ниже
(здесь и ниже  – мера Лебега-Стилтьеса, с функцией распределения F) справедливо равенство
– мера Лебега-Стилтьеса, с функцией распределения F) справедливо равенство
 . (1)
. (1)
В данном случае  имеет точки разрыва 0; 1 и 4 со скачками 3; 5 и
имеет точки разрыва 0; 1 и 4 со скачками 3; 5 и
–1 соответственно, а  почти всюду. Кроме того, в силу непрерывности меры снизу, имеем:
почти всюду. Кроме того, в силу непрерывности меры снизу, имеем:  , и аналогично,
, и аналогично, 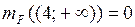 (другими словами, мера
(другими словами, мера  сосредоточена на отрезке
сосредоточена на отрезке  ). Значит, по формуле (1)
). Значит, по формуле (1)
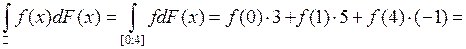
 .
.
2Проверить, что заданная на отрезке  функция
функция  не убывает и непрерывна слева. Рассмотреть меру Лебега-Стилтьеса
не убывает и непрерывна слева. Рассмотреть меру Лебега-Стилтьеса  , порожденную функцией
, порожденную функцией  . Найти:
. Найти:
а) меру каждого одноточечного множества;
б) меру канторова множества  ;
;
в) меру множества рациональных чисел, лежащих на отрезке  ;
;
г) интеграл 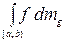 , если он существует.
, если он существует.
Пример 1. 

 ,
, 

Решение. Ясно, что  неубывающая функция и имеет точки разрыва
неубывающая функция и имеет точки разрыва  со скачками
со скачками  соответственно, в которых она непрерывна слева (рисунок 5).
соответственно, в которых она непрерывна слева (рисунок 5).
1) Если  и
и  , то (обоснуйте нижеследующие выкладки)
, то (обоснуйте нижеследующие выкладки)

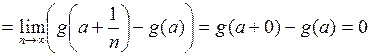 .
.

Рисунок 5 – График функции 
Если же  , то, рассуждая как выше, получим
, то, рассуждая как выше, получим
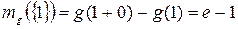 ,
,  .
.
2) По формуле (1)

 ,
,
поскольку  и
и  .
.
3) В силу счётности множества  множество рациональных чисел, лежащих на отрезке
множество рациональных чисел, лежащих на отрезке  , можно представить в виде
, можно представить в виде

 [0;9]
[0;9] 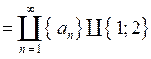 , где
, где  .
.
Учитывая сказанное в пункте 1), имеем  . Поэтому
. Поэтому

 .
.
г) Снова используя формулу (1) (которая справедлива и для промежутков вида [ a; b)), получаем

 =
=

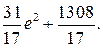
(Выше мы воспользовались тем, что 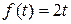 m -почти всюду, а потому
m -почти всюду, а потому


 , и
, и 
 .
. .
. , имеющей только точки разрыва первого рода
, имеющей только точки разрыва первого рода  со скачками
со скачками  соответственно и непрерывной слева, и для любой функции
соответственно и непрерывной слева, и для любой функции  (здесь и ниже
(здесь и ниже  – мера Лебега-Стилтьеса, с функцией распределения F) справедливо равенство
– мера Лебега-Стилтьеса, с функцией распределения F) справедливо равенство . (1)
. (1) имеет точки разрыва 0; 1 и 4 со скачками 3; 5 и
имеет точки разрыва 0; 1 и 4 со скачками 3; 5 и почти всюду. Кроме того, в силу непрерывности меры снизу, имеем:
почти всюду. Кроме того, в силу непрерывности меры снизу, имеем:  , и аналогично,
, и аналогично, 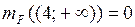 (другими словами, мера
(другими словами, мера  ). Значит, по формуле (1)
). Значит, по формуле (1)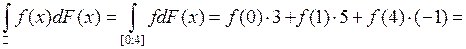
 .
. функция
функция  не убывает и непрерывна слева. Рассмотреть меру Лебега-Стилтьеса
не убывает и непрерывна слева. Рассмотреть меру Лебега-Стилтьеса  , порожденную функцией
, порожденную функцией  ;
; ;
;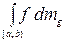 , если он существует.
, если он существует.

 ,
, 

 неубывающая функция и имеет точки разрыва
неубывающая функция и имеет точки разрыва  со скачками
со скачками  соответственно, в которых она непрерывна слева (рисунок 5).
соответственно, в которых она непрерывна слева (рисунок 5). и
и  , то (обоснуйте нижеследующие выкладки)
, то (обоснуйте нижеследующие выкладки)
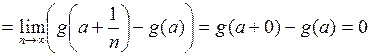 .
.

 , то, рассуждая как выше, получим
, то, рассуждая как выше, получим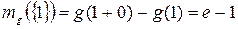 ,
,  .
.
 ,
, и
и  .
. множество рациональных чисел, лежащих на отрезке
множество рациональных чисел, лежащих на отрезке  , можно представить в виде
, можно представить в виде [0;9]
[0;9] 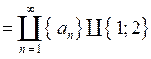 , где
, где  .
. . Поэтому
. Поэтому
 .
.
 =
=
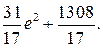
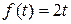 m -почти всюду, а потому
m -почти всюду, а потому



