 ,
,  ,
,  .
.
Решение. 1Найдем f (A).
1 способ. Заметим, что  . А так как функция f непрерывна, а множество А связно, то f принимает на А все свои промежуточные значения по теореме Больцано-Коши. Следовательно,
. А так как функция f непрерывна, а множество А связно, то f принимает на А все свои промежуточные значения по теореме Больцано-Коши. Следовательно, 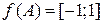 .
.
2 способ. Покажем, что 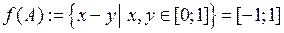 . В самом деле, с одной стороны,
. В самом деле, с одной стороны,
 ,
,
а потому  .
.
С другой стороны, если 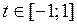 , то
, то
а) при  имеем
имеем  ;
;
б) при  имеем
имеем  .
.
Следовательно,  . Доказанные включения показывают, что
. Доказанные включения показывают, что 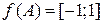
2 Имеем  , так как неравенство
, так как неравенство  равносильно неравенству
равносильно неравенству  .
.
3 Поскольку  Ø, то
Ø, то 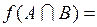 Ø.
Ø.
4 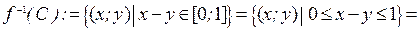
 и
и  .
.
Следовательно, данное множество представляет собой пересечение двух полуплоскостей, задаваемых неравенствами  и
и 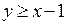 , т.е. полосу, заключенную между прямыми
, т.е. полосу, заключенную между прямыми  и
и  (рисунок 1).
(рисунок 1).
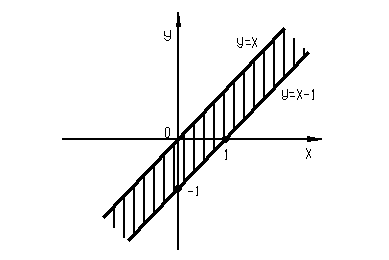
Рисунок 1 – Множество 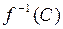
Очевидно, отображение f является сюръективным (почему?), не является инъективным (проверьте), а значит, не является и биективным.
3 Выяснить, является ли следующее множество конечным, счетным или множеством мощности континуум.
Пример 1. Множество всех замкнутых шаров в  натурального радиуса, координаты центров которых являются целыми числами.
натурального радиуса, координаты центров которых являются целыми числами.
Решение. Обозначим данное множество через М. Если каждому шару  из множества
из множества  поставить в соответствие точку
поставить в соответствие точку  из
из  (мы полагаем
(мы полагаем  ), то возникает отображение
), то возникает отображение 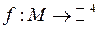 , которое, как легко проверить, инъективно (проверьте!). Следовательно, f есть биекция множества М на f (M). Но последнее множество счетно как бесконечное подмножество счетного множества
, которое, как легко проверить, инъективно (проверьте!). Следовательно, f есть биекция множества М на f (M). Но последнее множество счетно как бесконечное подмножество счетного множества  (оно бесконечно, поскольку эквивалентно бесконечному множеству М). Следовательно, будучи эквивалентным счетному множеству, множество М тоже счетно.
(оно бесконечно, поскольку эквивалентно бесконечному множеству М). Следовательно, будучи эквивалентным счетному множеству, множество М тоже счетно.
Пример 2. Множество действительных чисел из отрезка  , разложение которых в десятичную дробь неоднозначно.
, разложение которых в десятичную дробь неоднозначно.
Решение. Как известно, множество  всех чисел из отрезка
всех чисел из отрезка  , разложение которых в десятичную дробь неоднозначно, есть множество всех рациональных чисел из
, разложение которых в десятичную дробь неоднозначно, есть множество всех рациональных чисел из  , представимых в виде конечной десятичной дроби. (В этом случае число можно представить в виде бесконечной десятичной дроби двумя способами – с «хвостом» девяток и с «хвостом» нулей, например, 0,12 = 0,12(0) = 0,11(9)). Значит,
, представимых в виде конечной десятичной дроби. (В этом случае число можно представить в виде бесконечной десятичной дроби двумя способами – с «хвостом» девяток и с «хвостом» нулей, например, 0,12 = 0,12(0) = 0,11(9)). Значит, 
 . Но
. Но 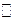 счетно. Поэтому
счетно. Поэтому  счетно как бесконечное подмножество счетного множества.
счетно как бесконечное подмножество счетного множества.
4 Выяснить, образует ли полуалгебру, алгебру,  -алгебру следующая система подмножеств данного множества Х.
-алгебру следующая система подмножеств данного множества Х.
Пример 1. Система всевозможных выпуклых многоугольников (включая и пустой многоугольник), содержащихся в квадрате  , (некоторые стороны могут не принадлежать многоугольнику).
, (некоторые стороны могут не принадлежать многоугольнику).
Решение. Обозначим данную систему через  и проверим для нее аксиомы алгебры:
и проверим для нее аксиомы алгебры:
1) пересечение двух выпуклых многоугольников, очевидно, является выпуклым многоугольником (выпуклый многоугольник есть пересечение конечного числа полуплоскостей), т. е. принадлежит  ;
;
2) дополнение до Х выпуклого многоугольника, лежащего строго внутри Х, как легко видеть, не является выпуклым многоугольником, т. е. не принадлежит  . Следовательно,
. Следовательно,  - не алгебра (а потому и не
- не алгебра (а потому и не  -алгебра).
-алгебра).
С другой стороны, если М – выпуклый многоугольник, содержащийся в квадрате Х, то отрезки перпендикуляров, опущенных из его вершин на стороны квадрата, разбивают дополнение  на конечное число выпуклых многоугольников (сделайте рисунок, иллюстрирующий это построение). Таким образом,
на конечное число выпуклых многоугольников (сделайте рисунок, иллюстрирующий это построение). Таким образом,  удовлетворяет всем аксиомам полуалгебры.
удовлетворяет всем аксиомам полуалгебры.

 ,
,  ,
,  .
. . А так как функция f непрерывна, а множество А связно, то f принимает на А все свои промежуточные значения по теореме Больцано-Коши. Следовательно,
. А так как функция f непрерывна, а множество А связно, то f принимает на А все свои промежуточные значения по теореме Больцано-Коши. Следовательно, 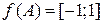 .
.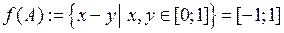 . В самом деле, с одной стороны,
. В самом деле, с одной стороны, ,
, .
.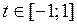 , то
, то имеем
имеем  ;
; имеем
имеем  .
. . Доказанные включения показывают, что
. Доказанные включения показывают, что  , так как неравенство
, так как неравенство  равносильно неравенству
равносильно неравенству  .
. Ø, то
Ø, то 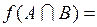 Ø.
Ø.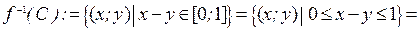
 и
и  .
. и
и 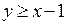 , т.е. полосу, заключенную между прямыми
, т.е. полосу, заключенную между прямыми  и
и  (рисунок 1).
(рисунок 1).
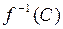
 натурального радиуса, координаты центров которых являются целыми числами.
натурального радиуса, координаты центров которых являются целыми числами. из множества
из множества  поставить в соответствие точку
поставить в соответствие точку  из
из  (мы полагаем
(мы полагаем  ), то возникает отображение
), то возникает отображение 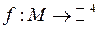 , которое, как легко проверить, инъективно (проверьте!). Следовательно, f есть биекция множества М на f (M). Но последнее множество счетно как бесконечное подмножество счетного множества
, которое, как легко проверить, инъективно (проверьте!). Следовательно, f есть биекция множества М на f (M). Но последнее множество счетно как бесконечное подмножество счетного множества  , разложение которых в десятичную дробь неоднозначно.
, разложение которых в десятичную дробь неоднозначно.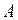 всех чисел из отрезка
всех чисел из отрезка 
 . Но
. Но  счетно как бесконечное подмножество счетного множества.
счетно как бесконечное подмножество счетного множества. -алгебру следующая система подмножеств данного множества Х.
-алгебру следующая система подмножеств данного множества Х. , (некоторые стороны могут не принадлежать многоугольнику).
, (некоторые стороны могут не принадлежать многоугольнику). и проверим для нее аксиомы алгебры:
и проверим для нее аксиомы алгебры: на конечное число выпуклых многоугольников (сделайте рисунок, иллюстрирующий это построение). Таким образом,
на конечное число выпуклых многоугольников (сделайте рисунок, иллюстрирующий это построение). Таким образом, 


