1 Пусть  – конечная мера, определенная на алгебре
– конечная мера, определенная на алгебре  подмножеств множества
подмножеств множества  ;
;  . Докажите указанное соотношение.
. Докажите указанное соотношение.
Пример 1.  .
.
Решение. Так как
 ,
,
 ,
, 
(рисунок 2), то по свойству конечной аддитивности меры получим
 , (1)
, (1)
 , (2)
, (2)
 . (3)
. (3)

Рисунок 2 – Множества 
Выразив  и
и  из (2) и (3) и подставив полученные выражения в (1), после преобразований получим
из (2) и (3) и подставив полученные выражения в (1), после преобразований получим
 .
.
2 Пусть 
 ,
,  – полуалгебра стрелок. Рассмотрим функцию на
– полуалгебра стрелок. Рассмотрим функцию на  , задаваемую равенствами
, задаваемую равенствами
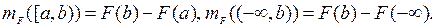 (1)
(1)
При каких значениях параметра  эти формулы задают: а) конечно-аддитивную меру; б)
эти формулы задают: а) конечно-аддитивную меру; б)  -аддитивную меру? Если мера не является
-аддитивную меру? Если мера не является  -аддитивной, то указать множество
-аддитивной, то указать множество  и его разбиение
и его разбиение  , такое, что
, такое, что 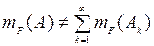 .
.
Пример 1. 
где n пробегает множество  целых чисел.
целых чисел.
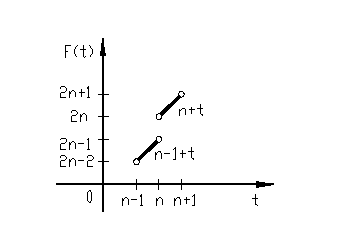
Рисунок 3 – Фрагмент графика функции 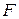 на множестве
на множестве  \
\ 
Решение 1 Легко видеть, что формулы (1) задают конечно-аддитивную меру тогда и только тогда, когда 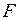 - неубывающая функция. Мы видим (рисунок 3), что на множестве
- неубывающая функция. Мы видим (рисунок 3), что на множестве  \
\  функция
функция 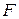 не убывает. Для того чтобы эта функция не убывала на всем
не убывает. Для того чтобы эта функция не убывала на всем  , необходимо и достаточно, чтобы
, необходимо и достаточно, чтобы  выполнялись условия
выполнялись условия  , то есть
, то есть  , или
, или  . Итак, данная мера конечно-аддитивна тогда и только тогда, когда
. Итак, данная мера конечно-аддитивна тогда и только тогда, когда  .
.
2 Как известно, данная формула будет задавать  -аддитивную меру тогда и только тогда, когда
-аддитивную меру тогда и только тогда, когда  неубывающая и непрерывная слева функция. Так как
неубывающая и непрерывная слева функция. Так как 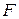 непрерывна на
непрерывна на  \
\  , то для этого необходимо и достаточно, чтобы
, то для этого необходимо и достаточно, чтобы 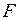 была непрерывна слева в точках
была непрерывна слева в точках 
 , то есть
, то есть  , или
, или  . Отсюда
. Отсюда  .
.
3 Пусть теперь  , то есть
, то есть  . Тогда мера
. Тогда мера  не является
не является  -аддитивной. Возьмем точку разрыва функции
-аддитивной. Возьмем точку разрыва функции 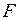 ,например,
,например, 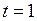 , и рассмотрим множества
, и рассмотрим множества
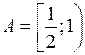 ,
,  .
.
Тогда  (проверьте), но
(проверьте), но

 .
.
А в то же время

 ,
,
так как  .
.
3 Выяснить, является ли данное множество  измеримым и найти его лебегову меру, если:
измеримым и найти его лебегову меру, если:
Пример 1.  , а
, а  =
=  .
.
Решение. Для любого рационального q уравнение  имеет счетное или пустое множество решений
имеет счетное или пустое множество решений  (найдите эти решения). Следовательно, множество
(найдите эти решения). Следовательно, множество  счетно. Заметим, что
счетно. Заметим, что 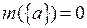 для любого а из
для любого а из  (докажите). Значит, А измеримо, причем
(докажите). Значит, А измеримо, причем  (объясните, почему).
(объясните, почему).
Пример 2. Множество  состоит из точек отрезка
состоит из точек отрезка  , у которых существует десятичное представление, содержащее хотя бы одну цифру 2.
, у которых существует десятичное представление, содержащее хотя бы одну цифру 2.
Решение. В дальнейшем мы будем пользоваться следующими двумя свойствами меры Лебега на прямой:
 (2)
(2)
которые справедливы для любого числа х и любого измеримого множества А.
Заметим, что дополнение  состоит из чисел, у которых существует десятичное представление, не содержащее цифру 2. Найдем
состоит из чисел, у которых существует десятичное представление, не содержащее цифру 2. Найдем  . Пусть
. Пусть
 .
.
Тогда ясно, что  . Кроме того, множество
. Кроме того, множество  измеримо. Теперь заметим, что
измеримо. Теперь заметим, что  (объединение берется по всем цифрам n, отличным от 2). В самом деле,
(объединение берется по всем цифрам n, отличным от 2). В самом деле,  , где цифры
, где цифры 

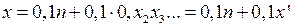 , где
, где 
 . Поэтому
. Поэтому  измеримо и
измеримо и 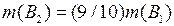 (мы воспользовались свойствами (2)). Аналогично получаем, что
(мы воспользовались свойствами (2)). Аналогично получаем, что  измеримо для любого
измеримо для любого  и
и  . Следовательно, по индукции
. Следовательно, по индукции  . Таким образом, множество
. Таким образом, множество  измеримо. Более того, поскольку
измеримо. Более того, поскольку  , то в силу свойства непрерывности меры сверху имеем
, то в силу свойства непрерывности меры сверху имеем
 .
.
А так как  то
то  (это означает, что вероятность того, что у случайно взятого числа
(это означает, что вероятность того, что у случайно взятого числа  в десятичной записи есть цифра 2, равна 1!).
в десятичной записи есть цифра 2, равна 1!).

 – конечная мера, определенная на алгебре
– конечная мера, определенная на алгебре  подмножеств множества
подмножеств множества  ;
;  . Докажите указанное соотношение.
. Докажите указанное соотношение. .
. ,
, ,
, 
 , (1)
, (1) , (2)
, (2) . (3)
. (3)

 и
и  из (2) и (3) и подставив полученные выражения в (1), после преобразований получим
из (2) и (3) и подставив полученные выражения в (1), после преобразований получим
 ,
,  – полуалгебра стрелок. Рассмотрим функцию на
– полуалгебра стрелок. Рассмотрим функцию на  , задаваемую равенствами
, задаваемую равенствами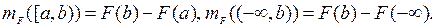 (1)
(1) эти формулы задают: а) конечно-аддитивную меру; б)
эти формулы задают: а) конечно-аддитивную меру; б)  -аддитивную меру? Если мера не является
-аддитивную меру? Если мера не является  и его разбиение
и его разбиение  , такое, что
, такое, что 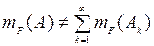 .
.
 целых чисел.
целых чисел.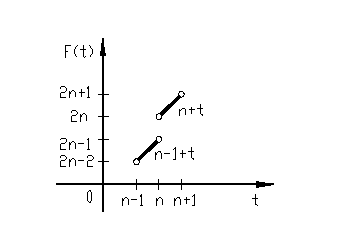
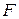 на множестве
на множестве 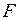 - неубывающая функция. Мы видим (рисунок 3), что на множестве
- неубывающая функция. Мы видим (рисунок 3), что на множестве  выполнялись условия
выполнялись условия  , то есть
, то есть  , или
, или  . Итак, данная мера конечно-аддитивна тогда и только тогда, когда
. Итак, данная мера конечно-аддитивна тогда и только тогда, когда  -аддитивную меру тогда и только тогда, когда
-аддитивную меру тогда и только тогда, когда  неубывающая и непрерывная слева функция. Так как
неубывающая и непрерывная слева функция. Так как 
 , или
, или  . Отсюда
. Отсюда  .
. , то есть
, то есть  . Тогда мера
. Тогда мера  не является
не является 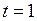 , и рассмотрим множества
, и рассмотрим множества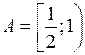 ,
,  .
. (проверьте), но
(проверьте), но
 .
.
 ,
, измеримым и найти его лебегову меру, если:
измеримым и найти его лебегову меру, если: , а
, а  =
=  .
. имеет счетное или пустое множество решений
имеет счетное или пустое множество решений  (найдите эти решения). Следовательно, множество
(найдите эти решения). Следовательно, множество  счетно. Заметим, что
счетно. Заметим, что 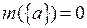 для любого а из
для любого а из  (докажите). Значит, А измеримо, причем
(докажите). Значит, А измеримо, причем  (объясните, почему).
(объясните, почему). состоит из точек отрезка
состоит из точек отрезка  , у которых существует десятичное представление, содержащее хотя бы одну цифру 2.
, у которых существует десятичное представление, содержащее хотя бы одну цифру 2. (2)
(2) состоит из чисел, у которых существует десятичное представление, не содержащее цифру 2. Найдем
состоит из чисел, у которых существует десятичное представление, не содержащее цифру 2. Найдем  . Пусть
. Пусть .
. . Кроме того, множество
. Кроме того, множество  измеримо. Теперь заметим, что
измеримо. Теперь заметим, что  (объединение берется по всем цифрам n, отличным от 2). В самом деле,
(объединение берется по всем цифрам n, отличным от 2). В самом деле,  , где цифры
, где цифры 

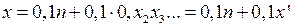 , где
, где 
 . Поэтому
. Поэтому  измеримо и
измеримо и 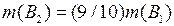 (мы воспользовались свойствами (2)). Аналогично получаем, что
(мы воспользовались свойствами (2)). Аналогично получаем, что  измеримо для любого
измеримо для любого  и
и  . Следовательно, по индукции
. Следовательно, по индукции  . Таким образом, множество
. Таким образом, множество  измеримо. Более того, поскольку
измеримо. Более того, поскольку  , то в силу свойства непрерывности меры сверху имеем
, то в силу свойства непрерывности меры сверху имеем .
. то
то  (это означает, что вероятность того, что у случайно взятого числа
(это означает, что вероятность того, что у случайно взятого числа  в десятичной записи есть цифра 2, равна 1!).
в десятичной записи есть цифра 2, равна 1!).


