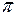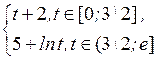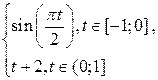Определение 1. Пусть функция  не убывает и непрерывна слева,
не убывает и непрерывна слева,  – мера Лебега-Стилтьеса с функцией распределения
– мера Лебега-Стилтьеса с функцией распределения 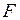 . Тогда интеграл
. Тогда интеграл  , (
, (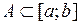 – борелевское множество) называется интегралом Лебега-Стилтьеса функции f и обозначается
– борелевское множество) называется интегралом Лебега-Стилтьеса функции f и обозначается
 .
.
При этом 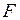 называют интегрирующей, а f – подынтегральной функцией.
называют интегрирующей, а f – подынтегральной функцией.
Понятие интеграла Лебега-Стилтьеса обобщается на более широкий класс интегрирующих функций.
Определение 2. Пусть F – функция на 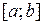 . Для разбиения
. Для разбиения  отрезка
отрезка 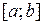 положим
положим

Функцию 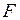 будем называть функцией ограниченной вариации (или функцией c ограниченным полным изменением) на
будем называть функцией ограниченной вариации (или функцией c ограниченным полным изменением) на 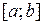 , если числа
, если числа 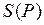 ограничены в совокупности. В этом случае число
ограничены в совокупности. В этом случае число

называется полной вариацией (или полным изменением) функции F на отрезке 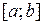 .
.
Класс всех функций c ограниченным полным изменением на 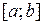 обозначим BV
обозначим BV 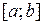 . Это векторное пространство относительно обычных (поточечных) операций над функциями.
. Это векторное пространство относительно обычных (поточечных) операций над функциями.
Известно, что BV 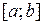 совпадает с классом функций, представимых в виде
совпадает с классом функций, представимых в виде  , где функции
, где функции 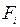 определены на отрезке
определены на отрезке 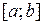 и не убывают (теорема Жордана). Это представление называется разложением Жордана функции F.
и не убывают (теорема Жордана). Это представление называется разложением Жордана функции F.
Определение 3. Пусть F –функция на 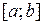 ограниченной вариации с разложением Жордана
ограниченной вариации с разложением Жордана  . Интеграл Лебега-Стилтьеса функции f с интегрирующей функцией F определяется следующим образом:
. Интеграл Лебега-Стилтьеса функции f с интегрирующей функцией F определяется следующим образом:
 .
.
1.4.1 Пусть  , и
, и

Вычислить  (таблица 1.4.1).
(таблица 1.4.1).
Таблица 1.4.1
1.4.2 Проверить, что заданная на отрезке  функция
функция  не убывает и непрерывна слева. Рассмотреть меру Лебега-Стилтьеса
не убывает и непрерывна слева. Рассмотреть меру Лебега-Стилтьеса  , порожденную функцией
, порожденную функцией  . Найти:
. Найти:
а) меру каждого одноточечного множества;
б) меру канторова множества С;
в) меру множества рациональных чисел, лежащих на отрезке  ;
;
г) интеграл 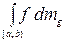 , если он существует (таблица 1.4.2).
, если он существует (таблица 1.4.2).
Таблица 1.4.2

 не убывает и непрерывна слева,
не убывает и непрерывна слева,  – мера Лебега-Стилтьеса с функцией распределения
– мера Лебега-Стилтьеса с функцией распределения 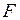 . Тогда интеграл
. Тогда интеграл  , (
, (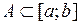 – борелевское множество) называется интегралом Лебега-Стилтьеса функции f и обозначается
– борелевское множество) называется интегралом Лебега-Стилтьеса функции f и обозначается .
.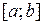 . Для разбиения
. Для разбиения  отрезка
отрезка 
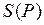 ограничены в совокупности. В этом случае число
ограничены в совокупности. В этом случае число
 , где функции
, где функции 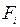 определены на отрезке
определены на отрезке  .
. , и
, и
 (таблица 1.4.1).
(таблица 1.4.1).


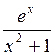









 функция
функция  не убывает и непрерывна слева. Рассмотреть меру Лебега-Стилтьеса
не убывает и непрерывна слева. Рассмотреть меру Лебега-Стилтьеса  , порожденную функцией
, порожденную функцией 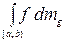 , если он существует (таблица 1.4.2).
, если он существует (таблица 1.4.2).