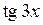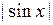Мера. Меры на 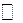
Определение 1. Пусть  есть полуалгебра подмножеств множества
есть полуалгебра подмножеств множества  . Отображение
. Отображение  , отличное от тождественной
, отличное от тождественной 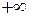 , называется мерой
, называется мерой  или
или  - аддитивной мерой), если оно удовлетворяет следующему условию:
- аддитивной мерой), если оно удовлетворяет следующему условию:
если 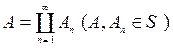 , то
, то  (
( - аддитивность).
- аддитивность).
Если же вместо условия  - аддитивности выполняется следующее более слабое условие:
- аддитивности выполняется следующее более слабое условие:
если 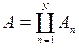
 , то
, то 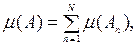
то  называется конечно-аддитивной мерой.
называется конечно-аддитивной мерой.
Теорема 1 (свойства мер). Мера  на алгебре
на алгебре  подмножеств множества
подмножеств множества  обладает следующими свойствами:
обладает следующими свойствами:
1)  -полуаддитивность: если
-полуаддитивность: если  , то
, то  ;
;
2) непрерывность снизу:
 ;
;
3) непрерывность сверху:
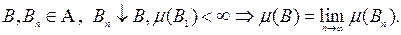
Система множеств
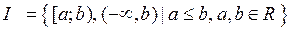
называется полуалгеброй стрелок.
Определение 2. Пусть  – неубывающая функция. Мера Лебега-Стилтьеса
– неубывающая функция. Мера Лебега-Стилтьеса 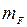 определяется на полуалгебре стрелок равенствами
определяется на полуалгебре стрелок равенствами 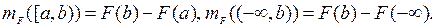
При этом 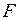 называется функцией распределения меры
называется функцией распределения меры 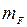 (или производящей функцией).
(или производящей функцией).
Определение 3. При  мера
мера 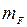 называется мерой Лебега на прямой и обозначается
называется мерой Лебега на прямой и обозначается 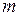 .
.
Теорема 2. Мера Лебега-Стилтьеса 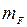
 - аддитивна тогда и только тогда, когда ее функция распределения F непрерывна слева. В частности, мера Лебега
- аддитивна тогда и только тогда, когда ее функция распределения F непрерывна слева. В частности, мера Лебега  - аддитивна.
- аддитивна.
1.2.1 Пусть  – конечная мера, определенная на алгебре
– конечная мера, определенная на алгебре  подмножеств множества
подмножеств множества  ;
;  . Докажите следующие соотношения:
. Докажите следующие соотношения:
Вариант 1.
 Ø
Ø  .
.
Вариант 2.
 .
.
Вариант 3.
 .
.
Вариант 4.
 .
.
Вариант 5.
 .
.
Вариант 6.
Если  , то
, то  .
.
Вариант 7.

 .
.
Вариант 8.
 .
.
Вариант 9.
 .
.
Вариант 10.
 .
.
Вариант 11. Если  то
то 
 .
.
Вариант 12.  Ø
Ø
( - симметрическая разность множеств E и F.).
- симметрическая разность множеств E и F.).
1.2.2 Пусть 
 ,
,  – полуалгебра стрелок. Рассмотрим функцию на
– полуалгебра стрелок. Рассмотрим функцию на  , задаваемую равенствами
, задаваемую равенствами
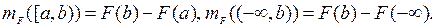
При каких значениях параметра  эти формулы задают: а) конечно-аддитивную меру; б)
эти формулы задают: а) конечно-аддитивную меру; б)  -аддитивную меру? Если мера не является
-аддитивную меру? Если мера не является  -аддитивной, то указать множество
-аддитивной, то указать множество  и его разбиение
и его разбиение  , такое, что
, такое, что 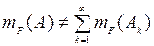 (таблица 1.2.2).
(таблица 1.2.2).
Таблица 1.2.2
1.2.3 Выяснить, является ли множество  измеримым и найти его лебегову меру, если
измеримым и найти его лебегову меру, если 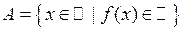 (таблица 1.2.3).
(таблица 1.2.3).
Таблица 1.2.3

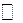
 есть полуалгебра подмножеств множества
есть полуалгебра подмножеств множества  . Отображение
. Отображение  , отличное от тождественной
, отличное от тождественной 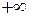 , называется мерой
, называется мерой  или
или  - аддитивной мерой), если оно удовлетворяет следующему условию:
- аддитивной мерой), если оно удовлетворяет следующему условию: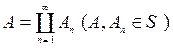 , то
, то  (
(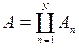
 , то
, то 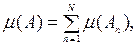
 называется конечно-аддитивной мерой.
называется конечно-аддитивной мерой. подмножеств множества
подмножеств множества  , то
, то  ;
; ;
;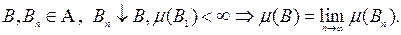
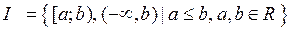
 – неубывающая функция. Мера Лебега-Стилтьеса
– неубывающая функция. Мера Лебега-Стилтьеса 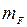 определяется на полуалгебре стрелок равенствами
определяется на полуалгебре стрелок равенствами 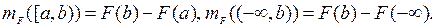
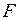 называется функцией распределения меры
называется функцией распределения меры  мера
мера 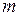 .
. - аддитивна тогда и только тогда, когда ее функция распределения F непрерывна слева. В частности, мера Лебега
- аддитивна тогда и только тогда, когда ее функция распределения F непрерывна слева. В частности, мера Лебега  подмножеств множества
подмножеств множества  . Докажите следующие соотношения:
. Докажите следующие соотношения: Ø
Ø  .
. .
. .
. .
. .
. , то
, то  .
.
 .
. .
. .
. .
. то
то 
 .
. Ø
Ø - симметрическая разность множеств E и F.).
- симметрическая разность множеств E и F.).
 ,
,  – полуалгебра стрелок. Рассмотрим функцию на
– полуалгебра стрелок. Рассмотрим функцию на  , задаваемую равенствами
, задаваемую равенствами эти формулы задают: а) конечно-аддитивную меру; б)
эти формулы задают: а) конечно-аддитивную меру; б)  -аддитивную меру? Если мера не является
-аддитивную меру? Если мера не является  и его разбиение
и его разбиение  , такое, что
, такое, что 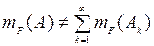 (таблица 1.2.2).
(таблица 1.2.2).

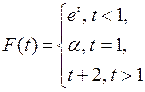
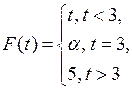

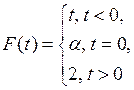






 измеримым и найти его лебегову меру, если
измеримым и найти его лебегову меру, если 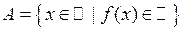 (таблица 1.2.3).
(таблица 1.2.3).