1 Докажите, что функция  является простой, а затем, пользуясь определением интеграла от простой функции, вычислите
является простой, а затем, пользуясь определением интеграла от простой функции, вычислите  .
.
Пример 1. Множество  есть отрезок
есть отрезок  .
.
Решение. Легко подсчитать, что
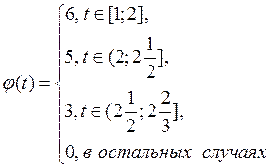
(произведите эти подсчеты). Следовательно, график функции 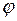 имеет вид
имеет вид
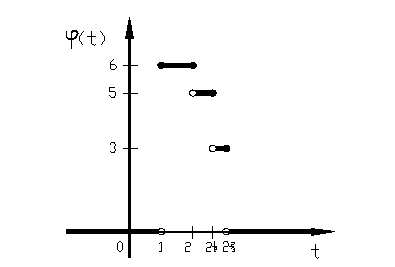
Рисунок 4 – График функции 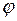
Таким образом, каноническое представление этой функции есть
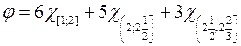
(объясните, почему). Поскольку индикатор  измерим, когда (и только когда) измеримо множество А, то данная функция измерима, как линейная комбинация измеримых, а потому является простой, причем по определению
измерим, когда (и только когда) измеримо множество А, то данная функция измерима, как линейная комбинация измеримых, а потому является простой, причем по определению

 .
.
2 Для функции  :
:
а) выяснить, является ли  ограниченной;
ограниченной;
б) найти меру Лебега множества ее точек разрыва;
в) определить, существует ли от нее собственный или несобственный интеграл Римана;
г) выяснить, измерима ли  ;
;
д) найти интеграл Лебега  , если он существует.
, если он существует.
Пример 1 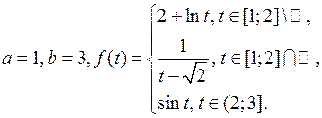
Решение. 1) Поскольку функция  не ограничена на множестве
не ограничена на множестве  (докажите), то
(докажите), то  неограниченная функция.
неограниченная функция.
Покажем, что множество точек разрыва функции  есть отрезок
есть отрезок  , из которого удалена некоторая точка а. Пусть
, из которого удалена некоторая точка а. Пусть  . Рассмотрим последовательность точек
. Рассмотрим последовательность точек  , такую, что
, такую, что  при
при  . Тогда
. Тогда  , если
, если  , и
, и  , если
, если  .
.
С другой стороны, если мы возьмем последовательность точек  , такую, что
, такую, что  ,то будем иметь
,то будем иметь  при
при  . Следовательно, если
. Следовательно, если  , то
, то 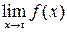 не существует, а если
не существует, а если  , то существует
, то существует 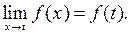
Резюмируя, получаем, что функция  разрывна в тех и только тех точках
разрывна в тех и только тех точках  , для которых
, для которых  . Но уравнение
. Но уравнение  имеет единственное решение
имеет единственное решение  (докажите это, используя теорему о промежуточном значении и монотонность левой части). Таким образом, множество точек разрыва функции f есть
(докажите это, используя теорему о промежуточном значении и монотонность левой части). Таким образом, множество точек разрыва функции f есть  , а, стало быть, мера множества точек разрыва функции
, а, стало быть, мера множества точек разрыва функции  равна 1.
равна 1.
3) Из результата пункта 1 следует, что функция  не интегрируема по Риману на отрезке
не интегрируема по Риману на отрезке  ..
..
Что касается несобственного интеграла, то он не существует, так как в силу критерия Лебега не существует риманов интеграл  (см. определение несобственного интеграла от неограниченной функции, определенной на конечном промежутке).
(см. определение несобственного интеграла от неограниченной функции, определенной на конечном промежутке).
4 Определение функции  можно переписать в виде
можно переписать в виде
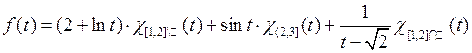
(подумайте, почему). Поскольку измеримые функции образуют алгебру, а непрерывные функции и индикаторы измеримых множеств измеримы, из этого равенства следует, что функция f тоже измерима.
5 Так как  , то
, то
 п. в.
п. в.
Поэтому интеграл Лебега для функции  по отрезку
по отрезку  совпадает с интегралом Лебега (а потому и с интегралом Римана) для функции
совпадает с интегралом Лебега (а потому и с интегралом Римана) для функции  по этому отрезку. Следовательно,
по этому отрезку. Следовательно,
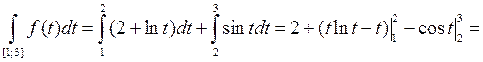
 .
.
3 Доказатьсуществование и вычислить  , где
, где  плоская мера Лебега,
плоская мера Лебега,  .
.
Пример 1. 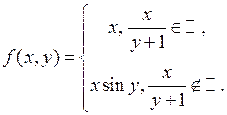
Решение. Докажем, что 
 - почти всюду на множестве
- почти всюду на множестве  . Действительно,
. Действительно,  , если
, если  , где
, где
 .
.
Далее, равенство  равносильно
равносильно 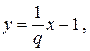
 , если
, если  , и
, и  ,
,  , если
, если  . Значит, множество N содержится в объединении счетного множества прямых
. Значит, множество N содержится в объединении счетного множества прямых  . А так как
. А так как 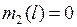 для любой прямой l, то
для любой прямой l, то 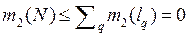 . Следовательно, существует интеграл
. Следовательно, существует интеграл


(мы восплользовались тем, что двойной интегрвал Римана функции g (x, y), если он существует, совпадает с интегралом от g (x, y) по плоской мере Лебега).
Тема 4

 является простой, а затем, пользуясь определением интеграла от простой функции, вычислите
является простой, а затем, пользуясь определением интеграла от простой функции, вычислите  .
.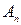 есть отрезок
есть отрезок  .
.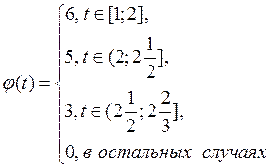
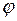 имеет вид
имеет вид
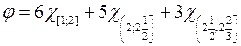
 измерим, когда (и только когда) измеримо множество А, то данная функция измерима, как линейная комбинация измеримых, а потому является простой, причем по определению
измерим, когда (и только когда) измеримо множество А, то данная функция измерима, как линейная комбинация измеримых, а потому является простой, причем по определению
 .
. :
: ограниченной;
ограниченной; , если он существует.
, если он существует.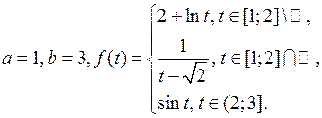
 не ограничена на множестве
не ограничена на множестве  (докажите), то
(докажите), то  неограниченная функция.
неограниченная функция. есть отрезок
есть отрезок  , из которого удалена некоторая точка а. Пусть
, из которого удалена некоторая точка а. Пусть  . Рассмотрим последовательность точек
. Рассмотрим последовательность точек  , такую, что
, такую, что  при
при  . Тогда
. Тогда  , если
, если  , и
, и  , если
, если  .
. , такую, что
, такую, что  ,то будем иметь
,то будем иметь  при
при  , то
, то 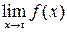 не существует, а если
не существует, а если  , то существует
, то существует 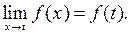
 имеет единственное решение
имеет единственное решение  (докажите это, используя теорему о промежуточном значении и монотонность левой части). Таким образом, множество точек разрыва функции f есть
(докажите это, используя теорему о промежуточном значении и монотонность левой части). Таким образом, множество точек разрыва функции f есть  , а, стало быть, мера множества точек разрыва функции
, а, стало быть, мера множества точек разрыва функции  ..
.. (см. определение несобственного интеграла от неограниченной функции, определенной на конечном промежутке).
(см. определение несобственного интеграла от неограниченной функции, определенной на конечном промежутке).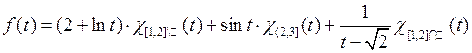
 , то
, то п. в.
п. в. совпадает с интегралом Лебега (а потому и с интегралом Римана) для функции
совпадает с интегралом Лебега (а потому и с интегралом Римана) для функции  по этому отрезку. Следовательно,
по этому отрезку. Следовательно,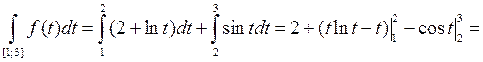
 .
. , где
, где  плоская мера Лебега,
плоская мера Лебега,  .
.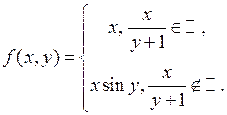

 - почти всюду на множестве
- почти всюду на множестве  . Действительно,
. Действительно,  , где
, где .
. равносильно
равносильно 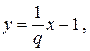
 , если
, если  , и
, и  ,
,  . Значит, множество N содержится в объединении счетного множества прямых
. Значит, множество N содержится в объединении счетного множества прямых  . А так как
. А так как 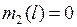 для любой прямой l, то
для любой прямой l, то 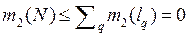 . Следовательно, существует интеграл
. Следовательно, существует интеграл



