Примеры решения типовых задач. 1. Найти сопряженный к оператору в гильбертовом пространстве .
1. Найти сопряженный к оператору Пример 1. Решение. Воспользуемся тем фактом, что
Другими словами,
В данном случае 1) В этом случае утверждение « 2) В этом случае утверждение «
2. Найти сопряженный к оператору Пример 1. Решение. В данном пространстве скалярное произведение задается следующим образом:
Следовательно,
Поскольку полученное выражение должно равняться
3. Если это возможно, приведите пример самосопряженного оператора Пример 1. Решение. Рассмотрим оператор Пример 2. Ответ: Данное множество не может быть точечным спектром самосопряженного оператора. Указание. Необходимо воспользоваться свойством спектра самосопряженного оператора в гильбертовом пространстве.
|

 в гильбертовом пространстве
в гильбертовом пространстве  .
.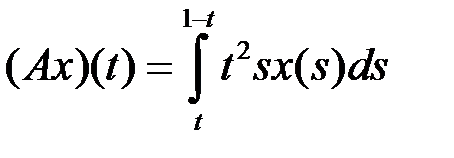 .
.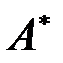 тоже является интегральным оператором, причем для ядер операторов
тоже является интегральным оператором, причем для ядер операторов  и
и  выполняется соотношение
выполняется соотношение . (1)
. (1)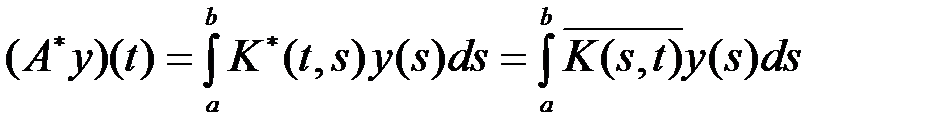 .
. , если
, если  находится между
находится между  и
и  , и
, и  в остальных случаях. В силу (1) должно выполняться
в остальных случаях. В силу (1) должно выполняться  , если
, если 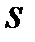 и
и 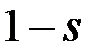 , и
, и  в остальных случаях. Возможно 2 случая:
в остальных случаях. Возможно 2 случая: . Тогда
. Тогда  .
. , т. е. тому, что
, т. е. тому, что 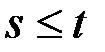 и
и  . Отсюда
. Отсюда  (объясните последнее равенство).
(объясните последнее равенство).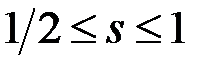 . Тогда
. Тогда  .
.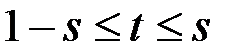 , т. е. тому, что
, т. е. тому, что  и
и  . Отсюда
. Отсюда  (мы воспользовались тем, что
(мы воспользовались тем, что  ). Поэтому
). Поэтому


 .
. в гильбертовом пространстве
в гильбертовом пространстве  с весом
с весом  , где
, где  .
.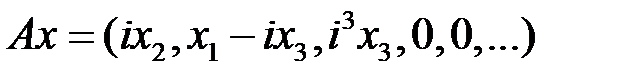 .
. .
.
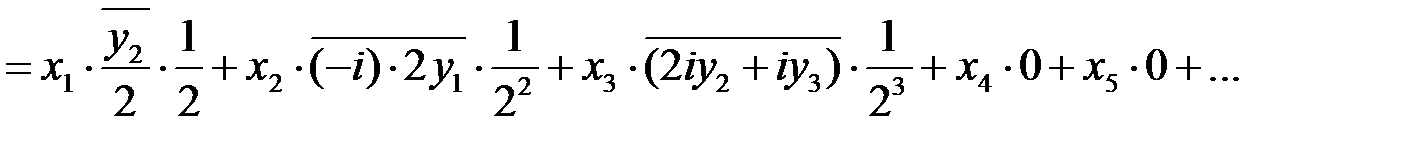 .
.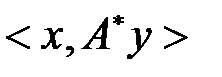 , то в силу единственности сопряженного оператора имеем
, то в силу единственности сопряженного оператора имеем .
. в гильбертовом пространстве, точечный спектр которого совпадает с данным множеством
в гильбертовом пространстве, точечный спектр которого совпадает с данным множеством  .
. .
. в пространстве
в пространстве  . Несложно проверить (сделайте это), что он является самосопряженным, и точечный спектр его совпадает с данным множеством
. Несложно проверить (сделайте это), что он является самосопряженным, и точечный спектр его совпадает с данным множеством  .
. .
.


