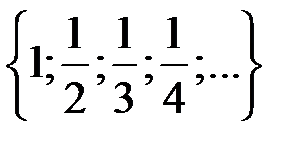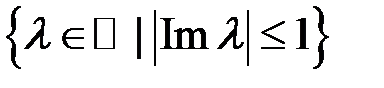Спектр линейного непрерывного оператора
Всюду далее Определение. Собственным значением оператора
имеет ненулевые решения. Эти решения называются собственными векторами оператора Определение. Множество всех собственных значений оператора Определение. Число Определение. Множесто регулярных точек обозначается Определение. Операторнозначная функция
называется резольвентой оператора Определение. Спектром оператора
Теорема. Спектр оператора Определение. Непрерывным спектром оператора Определение. Остаточным спектром оператора 4.2.1. Найти спектр данного оператора Таблица 4.2.1
4.2.2. Найти спектр и резольвентное множество данного оператора
Таблица 4.2.2
4.2.3. Найти собственные значения, точки непрерывного и точки остаточного спектров оператора
Таблица 4.2.3
4.2.4. Найти спектр оператора Таблица 4.2.4
Окончание таблицы 4.2.4
4.2.5. Выяснить, может ли множество
Таблица 4.2.5
|

 – комплексное банахово пространство,
– комплексное банахово пространство, 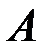 - линейный ограниченный оператор в
- линейный ограниченный оператор в  , при котором уравнение
, при котором уравнение
 .
.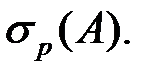
 имеет ограниченный обратный.
имеет ограниченный обратный. и называется резольвентным множеством оператора
и называется резольвентным множеством оператора 
 .
. тех
тех  из
из  , для которых множество
, для которых множество  плотно в
плотно в  тех
тех  , для которых множество
, для которых множество  не плотно в
не плотно в  (таблица 4.2.1).
(таблица 4.2.1).










 в пространстве
в пространстве 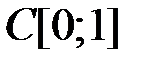 (таблица 4.2.2).
(таблица 4.2.2).









 в пространстве
в пространстве  , если
, если  (таблица 4.2.3).
(таблица 4.2.3).



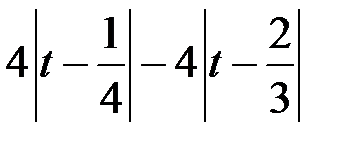






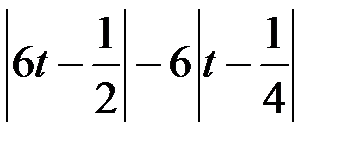
 в пространстве
в пространстве  , если
, если  (таблица 4.2.4).
(таблица 4.2.4).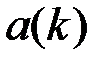







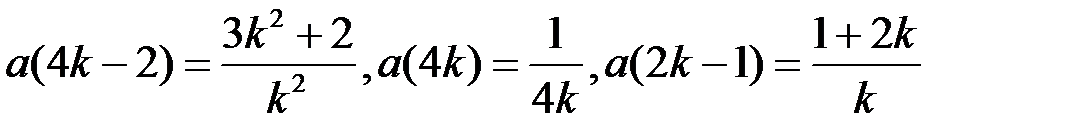


 быть спектром неко-торого линейного ограниченного оператора. В случае поло-жительного ответа привести пример такого оператора (таблица 4.2.5).
быть спектром неко-торого линейного ограниченного оператора. В случае поло-жительного ответа привести пример такого оператора (таблица 4.2.5).