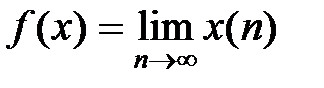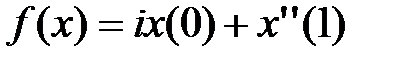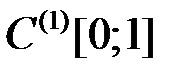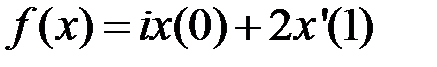Линейные ограниченные функционалы и операторы в нормированных пространствах
Определение. Пусть  – нормированное пространство над полем
– нормированное пространство над полем 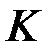 (
( ). Ограниченный линейный оператор
). Ограниченный линейный оператор  называется ограниченным (непрерывным) линейным функционалом.
называется ограниченным (непрерывным) линейным функционалом.
Пространство  ограниченных линейных функционалов на Х обозначается
ограниченных линейных функционалов на Х обозначается 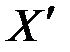 (или
(или  ) и называется сопряженным к Х.
) и называется сопряженным к Х.
Ниже для числа  через q будет обозначаться такое число, что
через q будет обозначаться такое число, что  (при
(при  считается, что
считается, что  ).
).
Теорема (об общем виде линейного ограниченного функционала в  ). Пусть
). Пусть 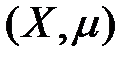 – пространство с
– пространство с  -конечной мерой,
-конечной мерой,  . Для любого ограниченного линейного функционала f на
. Для любого ограниченного линейного функционала f на  существует такое единственное
существует такое единственное  , что
, что
 ,
,
и обратно, любой функционал такого вида линеен и ограничен на  . При этом
. При этом 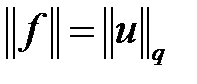 .
.
Примечание. Пространство  состоит из существенно ограниченных функций (функция
состоит из существенно ограниченных функций (функция  называется существенно ограниченной на отрезке
называется существенно ограниченной на отрезке  , если
, если 
 почти всюду на
почти всюду на  ). Норма в пространстве
). Норма в пространстве  задается следующим образом:
задается следующим образом:
 {
{ 

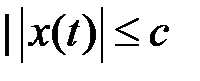 п.в. на
п.в. на  }.
}.
Следствие (об общем виде линейного ограниченного функционала в  ). Пусть
). Пусть  . Для любого ограниченного линейного функционала f на
. Для любого ограниченного линейного функционала f на  существует такое единственное
существует такое единственное  , что
, что
 ,
,
и обратно, любой функционал такого вида линеен и ограничен на 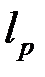 . При этом
. При этом  .
.
Теорема (об общем виде линейного ограниченного функционала в пространстве 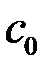 ). Для любого ограниченного линейного функционала f на
). Для любого ограниченного линейного функционала f на 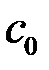 существует такое единственное
существует такое единственное  , что
, что
 ,
,
и обратно, любой функционал такого вида линеен и ограничен на  . При этом
. При этом  .
.
Ниже через  обозначается пространство функций ограниченной вариации на
обозначается пространство функций ограниченной вариации на  ,
, 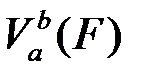 - вариация функции
- вариация функции  .
.
Теорема (об общем виде линейного ограниченного функционала в 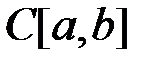 ). Для любого ограниченного линейного функционала f на
). Для любого ограниченного линейного функционала f на  существует единственная непрерывная слева функция
существует единственная непрерывная слева функция  , такая, что F (a) =0 и
, такая, что F (a) =0 и
 ,
,
и обратно, любой функционал такого вида линеен и ограничен на  . При этом
. При этом  .
.
4.1.1. Используя теорему об общем виде линейного ограниченного функционала в пространстве  , выяснить, задает ли данная формула линейный ограниченный функционал. В случае положительного ответа найти его норму (таблица 4.1.1).
, выяснить, задает ли данная формула линейный ограниченный функционал. В случае положительного ответа найти его норму (таблица 4.1.1).
Таблица 4.1.1
Окончание таблицы 4.1.1
4.1.2. Используя теорему об общем виде линейного ограниченного функционала в пространстве  , выяснить, задает ли данная формула линейный ограниченный функционал. В случае положительного ответа найти его норму (таблица 4.1.2).
, выяснить, задает ли данная формула линейный ограниченный функционал. В случае положительного ответа найти его норму (таблица 4.1.2).
Таблица 4.1.2
Окончание таблицы 4.1.2
4.1.3. Используя теорему об общем виде линейного ограниченного функционала в пространстве  , выяснить, задает ли данная формула линейный ограниченный функционал. В случае положительного ответа найти его норму (таблица 4.1.3).
, выяснить, задает ли данная формула линейный ограниченный функционал. В случае положительного ответа найти его норму (таблица 4.1.3).
Таблица 4.1.3
| Вариант
| p
| a
| b
| 
|
| 1
| 2
| 3
| 4
| 5
|
|
| 9/2
| - 1
|
| 
|
|
|
|
|
| 
|
|
|
|
|
| 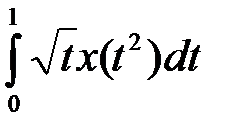
|
|
| 6/5
| - 1
|
| 
|
Окончание таблицы 4.1.3
| 1
| 2
| 3
| 4
| 5
|
|
|
|
|
| 
|
|
|
| - 1
|
| 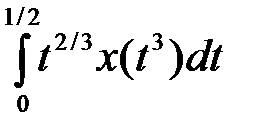
|
|
|
| -1
|
| 
|
|
|
|
|
| 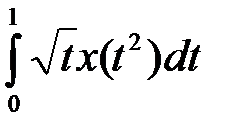
|
|
| 9/5
| -1
|
| 
|
|
| 5/4
|
|
| 
|
4.1.4. Используя теорему об общем виде линейного ограниченного функционала в пространстве  , выяснить, задает ли данная формула линейный ограниченный функционал. В случае положительного ответа найти его норму (таблица 4.1.4).
, выяснить, задает ли данная формула линейный ограниченный функционал. В случае положительного ответа найти его норму (таблица 4.1.4).
Таблица 4.1.4
Окончание таблицы 4.1.4
| 1
| 2
| 3
| 4
|
|
| - 3
|
| 
|
|
| - 2
|
| 
|
|
| -2
|
| 
|
|
| -1
|
| 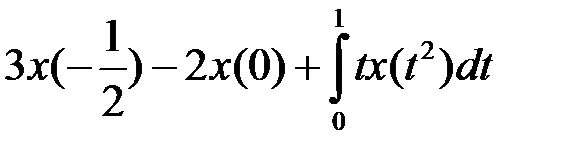
|
|
| -2
|
| 
|
|
| -4
|
| 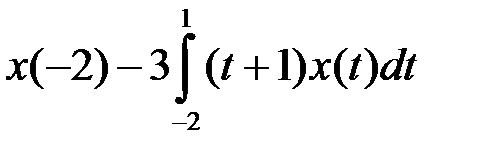
|
|
|
|
| 
|
4.1.5. Пусть Х – банахово пространство над полем К. Задает ли данная формула линейный ограниченный функционал  ? В случае положительного ответа найти его норму (таблица 4.1.5).
? В случае положительного ответа найти его норму (таблица 4.1.5).
Таблица 4.1.5
Окончание таблицы 4.1.5

 – нормированное пространство над полем
– нормированное пространство над полем 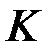 (
( ). Ограниченный линейный оператор
). Ограниченный линейный оператор  называется ограниченным (непрерывным) линейным функционалом.
называется ограниченным (непрерывным) линейным функционалом. ограниченных линейных функционалов на Х обозначается
ограниченных линейных функционалов на Х обозначается 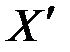 (или
(или  ) и называется сопряженным к Х.
) и называется сопряженным к Х. через q будет обозначаться такое число, что
через q будет обозначаться такое число, что  (при
(при  считается, что
считается, что  ).
). ). Пусть
). Пусть 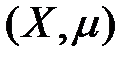 – пространство с
– пространство с  -конечной мерой,
-конечной мерой,  . Для любого ограниченного линейного функционала f на
. Для любого ограниченного линейного функционала f на  существует такое единственное
существует такое единственное  , что
, что ,
,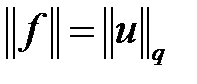 .
. состоит из существенно ограниченных функций (функция
состоит из существенно ограниченных функций (функция  называется существенно ограниченной на отрезке
называется существенно ограниченной на отрезке  , если
, если 
 почти всюду на
почти всюду на  ). Норма в пространстве
). Норма в пространстве  задается следующим образом:
задается следующим образом: {
{ 

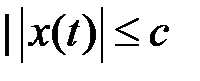 п.в. на
п.в. на  }.
}. ). Пусть
). Пусть  . Для любого ограниченного линейного функционала f на
. Для любого ограниченного линейного функционала f на  существует такое единственное
существует такое единственное  , что
, что ,
,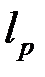 . При этом
. При этом  .
.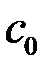 ). Для любого ограниченного линейного функционала f на
). Для любого ограниченного линейного функционала f на 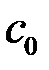 существует такое единственное
существует такое единственное  , что
, что ,
, . При этом
. При этом  .
. обозначается пространство функций ограниченной вариации на
обозначается пространство функций ограниченной вариации на  ,
, 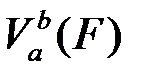 - вариация функции
- вариация функции  .
.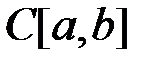 ). Для любого ограниченного линейного функционала f на
). Для любого ограниченного линейного функционала f на  существует единственная непрерывная слева функция
существует единственная непрерывная слева функция  , такая, что F (a) =0 и
, такая, что F (a) =0 и ,
, . При этом
. При этом  .
. , выяснить, задает ли данная формула линейный ограниченный функционал. В случае положительного ответа найти его норму (таблица 4.1.1).
, выяснить, задает ли данная формула линейный ограниченный функционал. В случае положительного ответа найти его норму (таблица 4.1.1).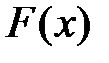

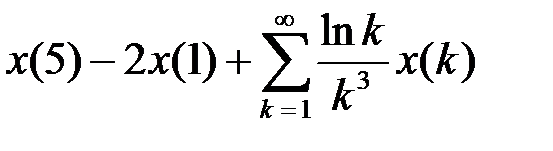








 , выяснить, задает ли данная формула линейный ограниченный функционал. В случае положительного ответа найти его норму (таблица 4.1.2).
, выяснить, задает ли данная формула линейный ограниченный функционал. В случае положительного ответа найти его норму (таблица 4.1.2).


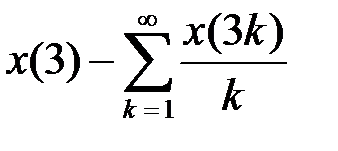



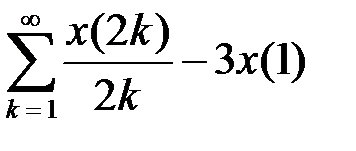






 , выяснить, задает ли данная формула линейный ограниченный функционал. В случае положительного ответа найти его норму (таблица 4.1.3).
, выяснить, задает ли данная формула линейный ограниченный функционал. В случае положительного ответа найти его норму (таблица 4.1.3).


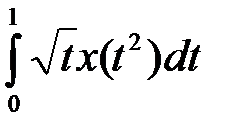


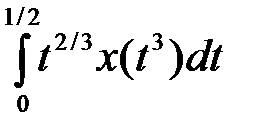



 , выяснить, задает ли данная формула линейный ограниченный функционал. В случае положительного ответа найти его норму (таблица 4.1.4).
, выяснить, задает ли данная формула линейный ограниченный функционал. В случае положительного ответа найти его норму (таблица 4.1.4).






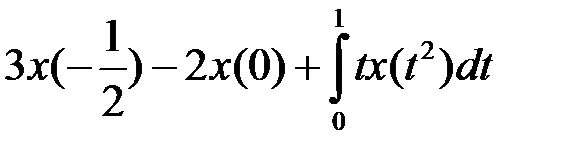

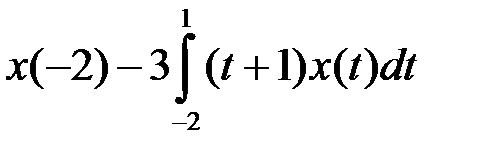

 ? В случае положительного ответа найти его норму (таблица 4.1.5).
? В случае положительного ответа найти его норму (таблица 4.1.5).