1. Выяснить, являются ли следующие операторы компактными в пространстве  .
.
Пример 1. 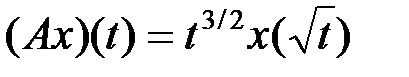 .
.
Решение. Докажем, что данный оператор не является компактным. Возьмем множество  . Оно ограничено в
. Оно ограничено в  . В то же время множество
. В то же время множество  не является предкомпактным в
не является предкомпактным в  , так как не удовлетворяет свойству Больцано-Вейерштрасса. В самом деле, из последовательности
, так как не удовлетворяет свойству Больцано-Вейерштрасса. В самом деле, из последовательности  нельзя извлечь сходящуюся в
нельзя извлечь сходящуюся в  подпоследовательность в силу того, что любая ее подпоследовательность будет иметь разрывный предел (какой?), а предел равномерно сходящейся последовательности непрерывных функций должен быть непрерывен. В соответствии с определением компактного оператора данный оператор не компактен.
подпоследовательность в силу того, что любая ее подпоследовательность будет иметь разрывный предел (какой?), а предел равномерно сходящейся последовательности непрерывных функций должен быть непрерывен. В соответствии с определением компактного оператора данный оператор не компактен.
Пример 2.  .
.
Решение. Представим данный оператор в виде  , где
, где
 ,
, 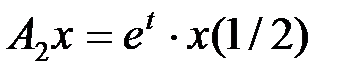 ,
,
и докажем, что операторы  и
и  компактны. Оператор
компактны. Оператор  компактен как интегральный оператор Фредгольма с непрерывным ядром.Компактность оператора
компактен как интегральный оператор Фредгольма с непрерывным ядром.Компактность оператора 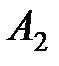 следует из того, что он является ограниченным оператором конечного ранга. Действительно, он ограничен, так как
следует из того, что он является ограниченным оператором конечного ранга. Действительно, он ограничен, так как
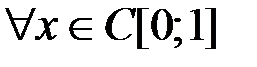
 ,
,
а с другой стороны образ оператора А есть
 ,
,
а потому
 ,
,
поскольку все функции 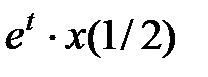 линейно выражаются через функцию
линейно выражаются через функцию  . Следовательно, оператор
. Следовательно, оператор  компактен как сумма компактных операторов.
компактен как сумма компактных операторов.
2. Выяснить, является ли оператор  компактным.
компактным.
Пример 1. 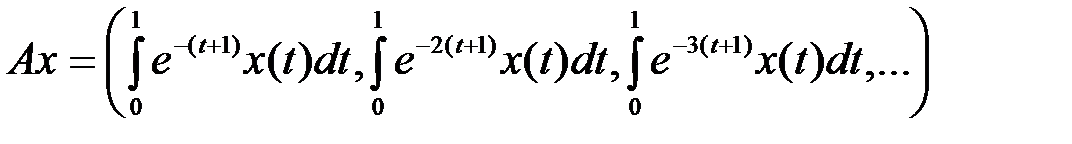 .
.
Решение. Докажем, что оператор  является компактным. Рассмотрим следующую последовательность линейных операторов
является компактным. Рассмотрим следующую последовательность линейных операторов  конечного ранга:
конечного ранга:

(образ оператора  содержится в n -мерном подпространстве пространства l 1 , состоящем из векторов вида
содержится в n -мерном подпространстве пространства l 1 , состоящем из векторов вида 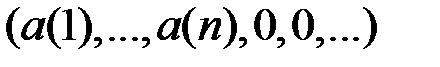 ).
).
Эти операторы ограничены. Действительно, 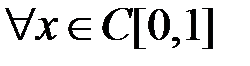

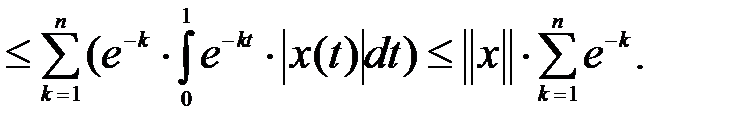
Следовательно, они компактны. Теперь компактность оператора А следует из того, что последовательность  сходится к А по норме, так как
сходится к А по норме, так как
 ,
,
а потому
 ,
,
поскольку остаток сходящегося ряда стремиться к нулю.
3. Выяснить, является ли оператор  компактным.
компактным.
Пример 1. 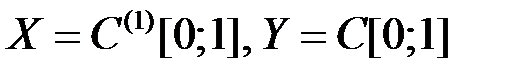 ,
,  .
.
Решение. Возьмем в  произвольное ограниченное множество М. Его ограниченность означает, что
произвольное ограниченное множество М. Его ограниченность означает, что 
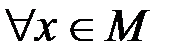
 .
.
Отсюда следует, что

 ,
, 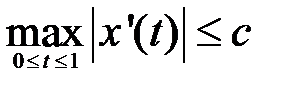 .
.
Рассмотрим теперь множество 
 . Оно равномерно ограничено, так как
. Оно равномерно ограничено, так как  . Кроме того,
. Кроме того, 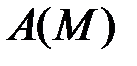 равностепенно непрерывно, так как по теореме Лагранжа
равностепенно непрерывно, так как по теореме Лагранжа 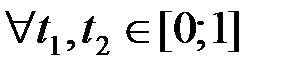
 .
.
В силу теоремы Арцела-Асколи множество  предкомпактно. Значит, оператор А компактен.
предкомпактно. Значит, оператор А компактен.
Пример 2.  ,
,  .
.
Решение. Возьмем ограниченное в  множество
множество
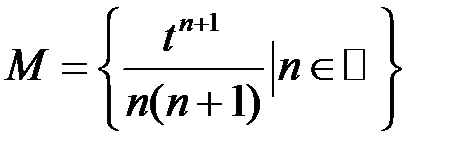
(проверьте ограниченность множества М). Множество  не является предкомпактным в пространстве
не является предкомпактным в пространстве  , так как не содержит сходящихся в
, так как не содержит сходящихся в  подпоследовательностей (т. е. не удовлетворяет свойству Больцано-Вейерштрасса). В самом деле, из сходимости последовательности в
подпоследовательностей (т. е. не удовлетворяет свойству Больцано-Вейерштрасса). В самом деле, из сходимости последовательности в 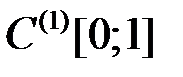 следует равномерная сходимость последовательности ее производных (проверьте это). А с другой стороны, из последовательности
следует равномерная сходимость последовательности ее производных (проверьте это). А с другой стороны, из последовательности  нельзя извлечь равномерно сходящуюся подпоследовательность (почему?). Значит, данный оператор не компактен.
нельзя извлечь равномерно сходящуюся подпоследовательность (почему?). Значит, данный оператор не компактен.

 .
.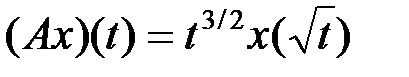 .
. . Оно ограничено в
. Оно ограничено в  . В то же время множество
. В то же время множество  не является предкомпактным в
не является предкомпактным в  , так как не удовлетворяет свойству Больцано-Вейерштрасса. В самом деле, из последовательности
, так как не удовлетворяет свойству Больцано-Вейерштрасса. В самом деле, из последовательности  нельзя извлечь сходящуюся в
нельзя извлечь сходящуюся в  подпоследовательность в силу того, что любая ее подпоследовательность будет иметь разрывный предел (какой?), а предел равномерно сходящейся последовательности непрерывных функций должен быть непрерывен. В соответствии с определением компактного оператора данный оператор не компактен.
подпоследовательность в силу того, что любая ее подпоследовательность будет иметь разрывный предел (какой?), а предел равномерно сходящейся последовательности непрерывных функций должен быть непрерывен. В соответствии с определением компактного оператора данный оператор не компактен. .
. , где
, где ,
, 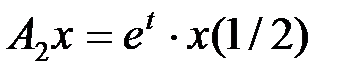 ,
, и
и  компактны. Оператор
компактны. Оператор  компактен как интегральный оператор Фредгольма с непрерывным ядром.Компактность оператора
компактен как интегральный оператор Фредгольма с непрерывным ядром.Компактность оператора 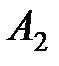 следует из того, что он является ограниченным оператором конечного ранга. Действительно, он ограничен, так как
следует из того, что он является ограниченным оператором конечного ранга. Действительно, он ограничен, так как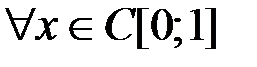
 ,
, ,
, ,
,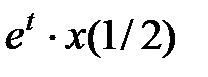 линейно выражаются через функцию
линейно выражаются через функцию  . Следовательно, оператор
. Следовательно, оператор  компактен как сумма компактных операторов.
компактен как сумма компактных операторов. компактным.
компактным.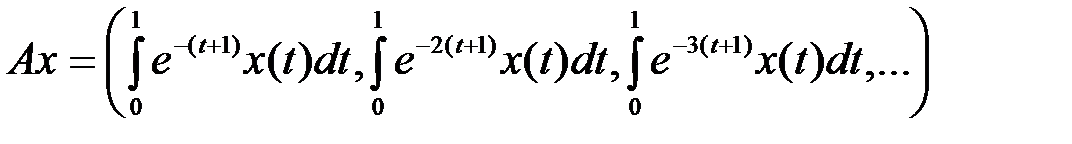 .
. является компактным. Рассмотрим следующую последовательность линейных операторов
является компактным. Рассмотрим следующую последовательность линейных операторов  конечного ранга:
конечного ранга:
 содержится в n -мерном подпространстве пространства l 1 , состоящем из векторов вида
содержится в n -мерном подпространстве пространства l 1 , состоящем из векторов вида 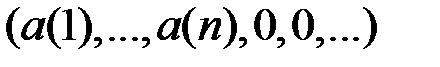 ).
).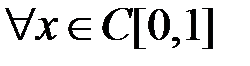

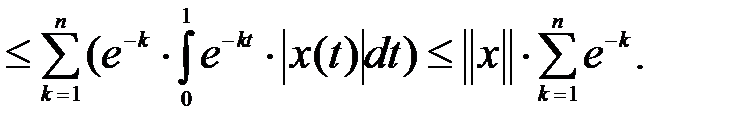
 сходится к А по норме, так как
сходится к А по норме, так как ,
, ,
, компактным.
компактным.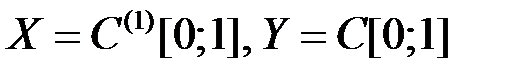 ,
,  .
. произвольное ограниченное множество М. Его ограниченность означает, что
произвольное ограниченное множество М. Его ограниченность означает, что 
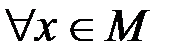
 .
.
 ,
, 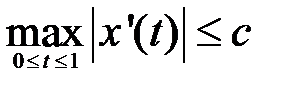 .
.
 . Оно равномерно ограничено, так как
. Оно равномерно ограничено, так как  . Кроме того,
. Кроме того, 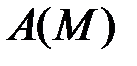 равностепенно непрерывно, так как по теореме Лагранжа
равностепенно непрерывно, так как по теореме Лагранжа 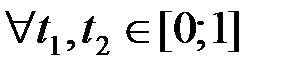
 .
. предкомпактно. Значит, оператор А компактен.
предкомпактно. Значит, оператор А компактен. ,
,  .
. множество
множество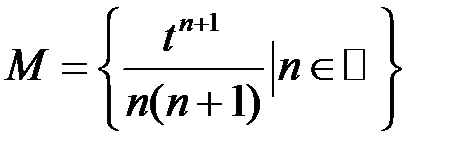
 не является предкомпактным в пространстве
не является предкомпактным в пространстве  , так как не содержит сходящихся в
, так как не содержит сходящихся в  подпоследовательностей (т. е. не удовлетворяет свойству Больцано-Вейерштрасса). В самом деле, из сходимости последовательности в
подпоследовательностей (т. е. не удовлетворяет свойству Больцано-Вейерштрасса). В самом деле, из сходимости последовательности в 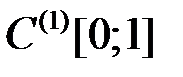 следует равномерная сходимость последовательности ее производных (проверьте это). А с другой стороны, из последовательности
следует равномерная сходимость последовательности ее производных (проверьте это). А с другой стороны, из последовательности  нельзя извлечь равномерно сходящуюся подпоследовательность (почему?). Значит, данный оператор не компактен.
нельзя извлечь равномерно сходящуюся подпоследовательность (почему?). Значит, данный оператор не компактен.


