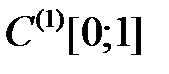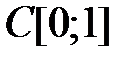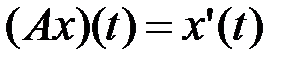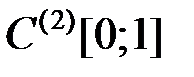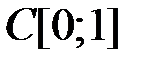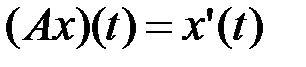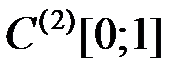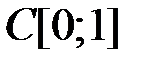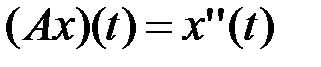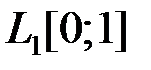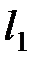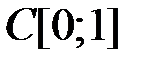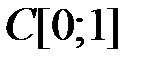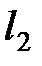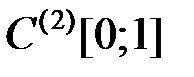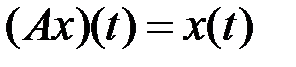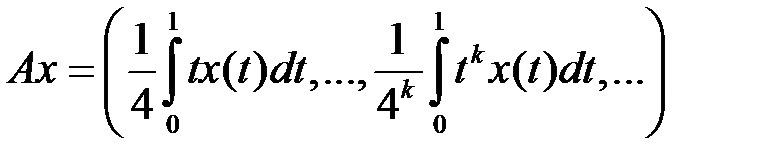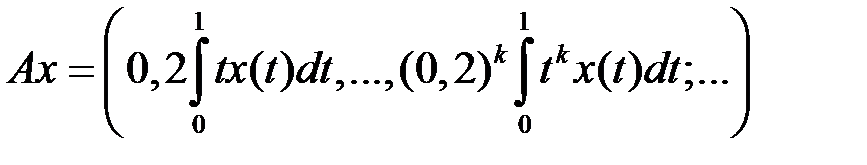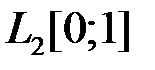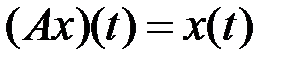Компактные операторы
Всюду ниже X,Y,Z – нормированные пространства над полем К ( Определение. Оператор А называется компактным, если он переводит ограниченные множества в предкомпактные. Множество всех компактных операторов Каждый компактный оператор ограничен, но обратное, вообще говоря, неверно. Теорема (свойства компактных операторов). 1) Множество 2) Пусть Определение. Оператор А называется оператором конечного ранга, если его образ Теорема. Ограниченный оператор конечного ранга компактен. Теорема. Интегральный оператор Фредгольма компактен в пространстве
4.3.1. Выяснить, является ли данный оператор компактным в пространстве
Таблица 4.3.1
4.3.2. Определить, является ли данный оператор компактным в пространстве
Таблица 4.3.2
4.3.3. Исследовать оператор на компактность в пространстве
Таблица 4.3.3
Окончание таблицы 4.3.3
4.3.4. Выяснить, является ли оператор
Таблица 4.3.4
|

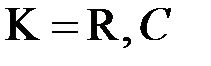 ),
), 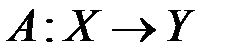 - линейный оператор.
- линейный оператор.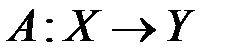 обозначается
обозначается 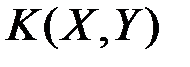 .
.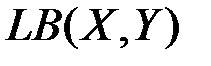 .
.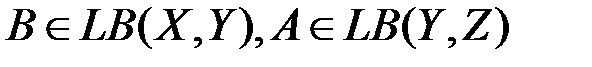 . Если один из операторов А или В компактен, то компактно и произведение АВ.
. Если один из операторов А или В компактен, то компактно и произведение АВ.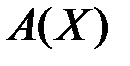 есть конечномерное пространство.
есть конечномерное пространство.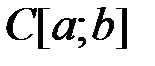 .
.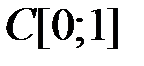 (таблица 4.3.1).
(таблица 4.3.1).
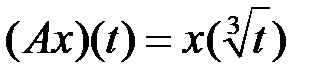

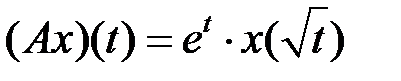

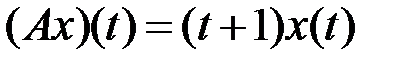

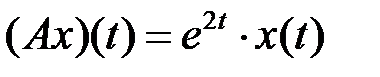
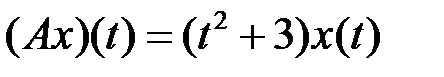

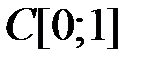 (таблица 4.3.2).
(таблица 4.3.2).
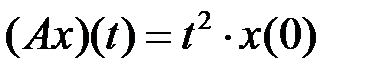
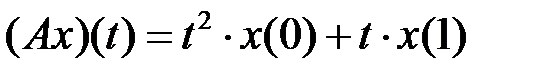
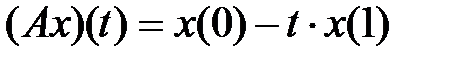
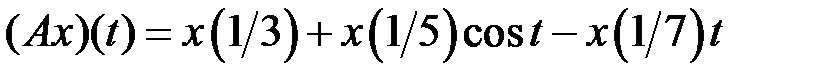
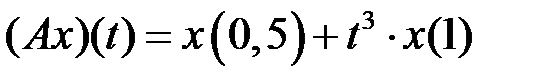

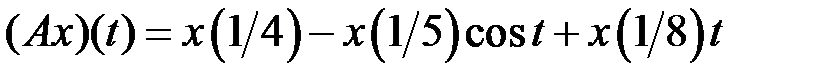
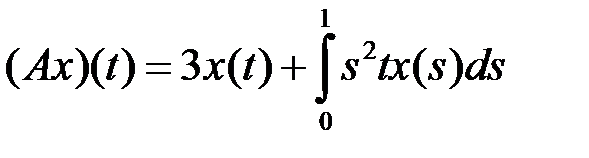
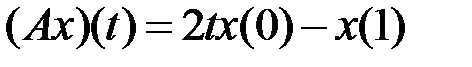
 (таблица 4.3.3).
(таблица 4.3.3).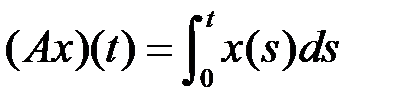

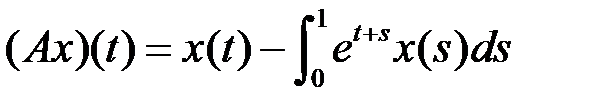
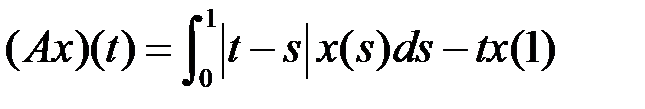
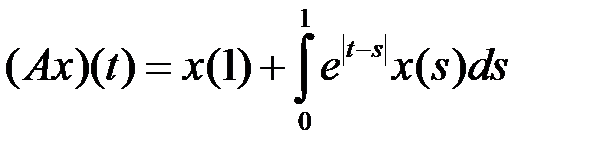
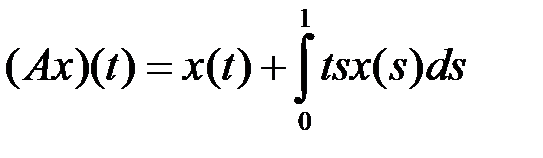
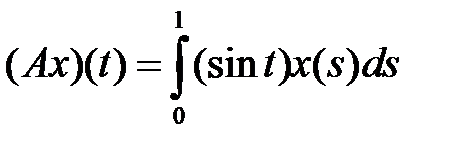
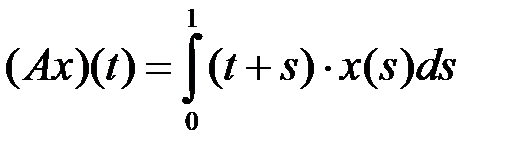
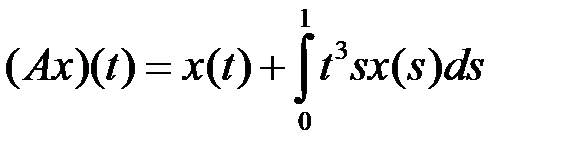
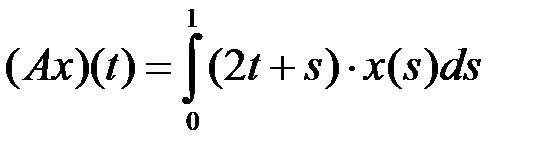
 компактным (таблица 4.3.4).
компактным (таблица 4.3.4).