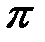Тема 5.3
Интегральные уравнения
В пространстве
где Наряду с уравнением (Ф) рассмотрим соответствующие ему однородное и сопряженное однородное уравнения:
Следующие результаты, связывающие между собой решения этих уравнений, носят название теорем Фредгольма. Теорема 1. Однородныеуравнения (Ф0) и (Ф*0) имеют одно и то же, причем конечное, число линейно независимых решений. Теорема 2. Уравнение (Ф) разрешимо для любого f тогда и только тогда, когда уравнение (Ф0) имеет только нулевое решение. Теорема 3. Уравнение (Ф) разрешимо для тех и только тех f, для которых равенство
выполняется для любого решения Теорема 4. Если функции k и f непрерывны, то теоремы Фредгольма справедливы и в пространстве C [ a,b ]. Будем далее рассматривать интегральное уравнение
5.3.1. Решить уравнение (1) при
Таблица 5.3.1
5.3.2. Не решая уравнения (1), определите, при каких
Таблица 5.3.2
5.3.3. Определить, при каких значениях параметра
Таблица 5.3.3
|
рассмотрим уравнени е
, (Ф)
, 
(уравнение Фредгольма 2 рода).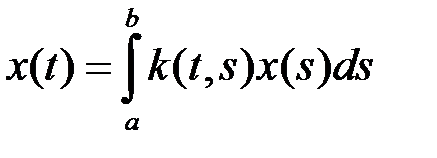
; (Ф0)
(Ф*0)
уравнения (Ф*0).
(1)
, если (таблица 5.3.1):
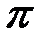
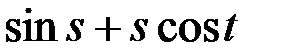
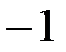
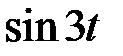
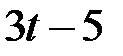
оно имеет решение в пространстве 
(в этой задаче мы полагаем 
) (таблица 5.3.2).
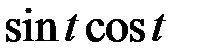
уравнение (1) разрешимо в пространстве 
при любой функции 
из 
(таблица 5.3.3).
