Примеры решения типовых задач. Решение. Нам нужно решить уравнение
1. Решить уравнение (1) при Пример 1. Решение. Нам нужно решить уравнение
то есть
Введем обозначения:
Тогда из (2) заключаем, что решение данного уравнения имеет вид
с неопределенными коэффициентами a и b. Для нахождения a и b подставим выражение (4) в систему (3):
или после вычисления интегралов в правых частях:
Отсюда
2. Не решая уравнения (1), определите, при каких Пример 1. Решение. Рассматривается уравнение
В соответствии с теоремой Фредгольма, данное уравнение разрешимо для тех и только тех Составим сопряженное однородное уравнение:
или
Введем обозначения
Тогда решение сопряженного однородного уравнения принимает вид
Подставив (7) в (6), получим систему уравнений
или после вычисления интегралов,
Отсюда
где С − произвольная постоянная. Значит, данное уравнение разрешимо для тех и только тех
3. При каких значениях параметра Пример 1. Решение. Рассматрим уравнение
В соответствии с теоремой Фредгольма данное уравнение разрешимо при любой функции Решим соответствующее однородное уравнение
или
Введем обозначения
Тогда
Подставив (9) в (8), получим
После вычисления интегралов получаем систему
или
Последняя система (а вместе с ней и соответствующее однородное уравнение) имеет только нулевое решение, если и только если
|

 .
. .
. ,
, . (2)
. (2)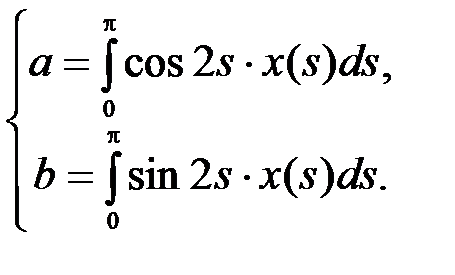 (3)
(3) (4)
(4)


 . Подставляя эти значения в (4), окончательно получаем
. Подставляя эти значения в (4), окончательно получаем  .
.
 оно имеет решение в пространстве
оно имеет решение в пространстве  (здесь мы полагаем
(здесь мы полагаем  ).
). .
. . (5)
. (5) , которые ортогональны любому решению сопряженного однородного уравнения.
, которые ортогональны любому решению сопряженного однородного уравнения.
 .
. (6)
(6) . (7)
. (7)

 , а − произвольная постоянная. Следовательно, решение сопряженного однородного уравнения есть
, а − произвольная постоянная. Следовательно, решение сопряженного однородного уравнения есть ,
, , для которых
, для которых .
. уравнение (1) разрешимо в пространстве
уравнение (1) разрешимо в пространстве  при любой функции
при любой функции  из
из  ?
? .
. .
. тогда и только тогда, когда соответствующее однородное уравнение имеет только нулевое решение.
тогда и только тогда, когда соответствующее однородное уравнение имеет только нулевое решение. ,
,
 (8)
(8) . (9)
. (9)



 и
и  . Значит, данное уравнение разрешимо в пространстве
. Значит, данное уравнение разрешимо в пространстве  при любой функции
при любой функции  .
.


