1. Найти спектр данного оператора  .
.
Пример 1. 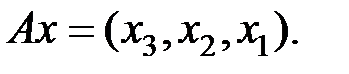
Решение. Известно, что спектр оператора в конечномерноли пространстве состоит из собственных значений. Таким образом, нас интересуют те значения параметра  , при которых уравнение
, при которых уравнение  имеет ненулевые решения. Но это уравнение равносильно следующей однородной системе линейных уравнений:
имеет ненулевые решения. Но это уравнение равносильно следующей однородной системе линейных уравнений:
 ,
,
главный определитель которой равен  . По следствию из правила Крамера эта система имеет ненулевое решение тогда и только тогда, когда ее главный определитель равен нулю. Решая уравнение
. По следствию из правила Крамера эта система имеет ненулевое решение тогда и только тогда, когда ее главный определитель равен нулю. Решая уравнение  , находим, что
, находим, что 
2. Найти спектр и резольвентное множество данного оператора А в пространстве  .
.
Пример 1.  .
.
Решение. Найдем сначала точечный спектр оператора А. Рассмотрим уравнение с неизвестной функцией х из 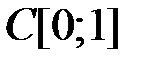
 , (1)
, (1)
то есть
 (2)
(2)
Требуется найти те значения параметра  , при которых это уравнение имеет ненулевое решение. Но из (2) следует, что
, при которых это уравнение имеет ненулевое решение. Но из (2) следует, что  при
при  , а тогда по непрерывности
, а тогда по непрерывности  при всех t. Значит, уравнение (2) не имеет ненулевых непрерывных решений ни при каких
при всех t. Значит, уравнение (2) не имеет ненулевых непрерывных решений ни при каких 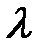 . Таким образом,
. Таким образом,  Ø.
Ø.
Рассмотрим теперь уравнение ( )
)
 , (3)
, (3)
то есть
 . (4)
. (4)
Резольвентное множество  состоит из тех значений
состоит из тех значений  , при которых оператор
, при которых оператор  обратим, т. е. при таких значениях
обратим, т. е. при таких значениях  уравнение (4) имеет единственное непрерывное решение х для любого непрерывного у.
уравнение (4) имеет единственное непрерывное решение х для любого непрерывного у.
Если  , то уравнение (4) однозначно разрешимо относительно
, то уравнение (4) однозначно разрешимо относительно 
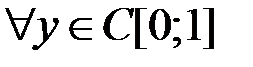 , а именно,
, а именно,  . В этом случае
. В этом случае  .
.
Если же  , то уравнение (4) разрешимо в пространстве
, то уравнение (4) разрешимо в пространстве 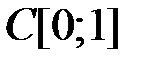 не для всех
не для всех  (например, оно не имеет решения при
(например, оно не имеет решения при  , так как из равенства (4) следует, что
, так как из равенства (4) следует, что 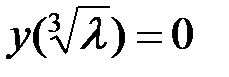 ). В этом случае
). В этом случае  .
.
Итак, 
 ,
,  .
.
Пример 2.  .
.
Решение. Рассмотрим уравнение  , т. е.
, т. е.
 . (5)
. (5)
Если 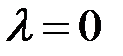 , то это уравнение имеет ненулевое решение (подходит любая непрерывная функция, для которой
, то это уравнение имеет ненулевое решение (подходит любая непрерывная функция, для которой  , например, функция
, например, функция  ). Значит,
). Значит, 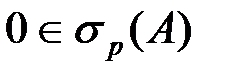 .
.
Если  , то, разделив на
, то, разделив на  ,из уравнения (5) выводим, что его решение должно иметь вид
,из уравнения (5) выводим, что его решение должно иметь вид  (k и b – неопределенные коэффициенты). Тогда
(k и b – неопределенные коэффициенты). Тогда  .
.
Подставив эти значения в (5), получим  , откуда
, откуда
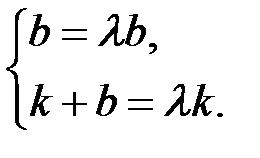
Из первого равенства системы следует, что  или
или  . В случае
. В случае  система имеет ненулевое решение (например
система имеет ненулевое решение (например  ). А если
). А если  , то система, как легко проверить, имеет только нулевое решение. Итак, уравнение (5) имеет ненулевое решение лишь при
, то система, как легко проверить, имеет только нулевое решение. Итак, уравнение (5) имеет ненулевое решение лишь при 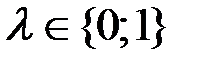 . Значит,
. Значит,  .
.
Для нахождения всего спектра будем рассуждать как в примере 1, то есть рассмотрим уравнение
 ,
,
или
 , (6)
, (6)
где  . Из (6) следует, что
. Из (6) следует, что
 .
.
Подставив в (6) значение  , получим
, получим  . Полагая в (6)
. Полагая в (6)  , находим, что
, находим, что
 .
.
Значит, если  , то решение уравнения (6) имеет вид
, то решение уравнения (6) имеет вид
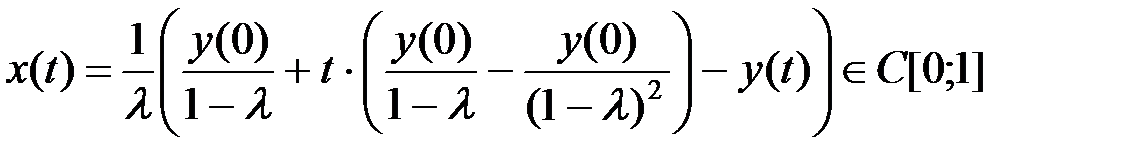 .
.
Таким образом, при  уравнение (6) однозначно разрешимо в
уравнение (6) однозначно разрешимо в  для любого у из
для любого у из 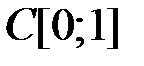 . Итак,
. Итак, 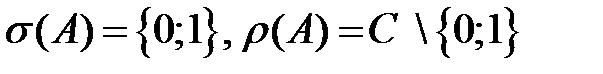 .
.
3. Найти собственные значения, точки непрерывного и точки остаточного спектров оператора А в пространстве  , если
, если  .
.
Пример 1.  .
.
Решение. Применяя к выражению  метод интервалов, получим
метод интервалов, получим
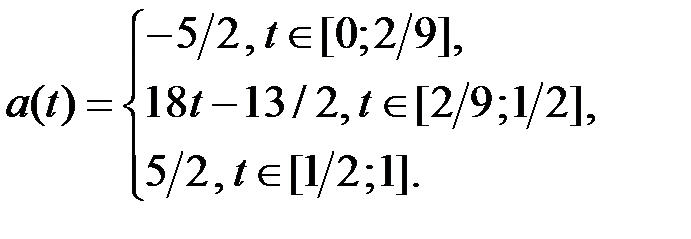
Отметим, что множество значений E (a)этой функции есть отрезок  (рисунок 8). Рассмотрим уравнение
(рисунок 8). Рассмотрим уравнение  , то есть
, то есть  , или
, или
 . (7)
. (7)
Если  , то уравнение (7) имеет только нулевое решение. Если
, то уравнение (7) имеет только нулевое решение. Если  , то
, то 
 .
.
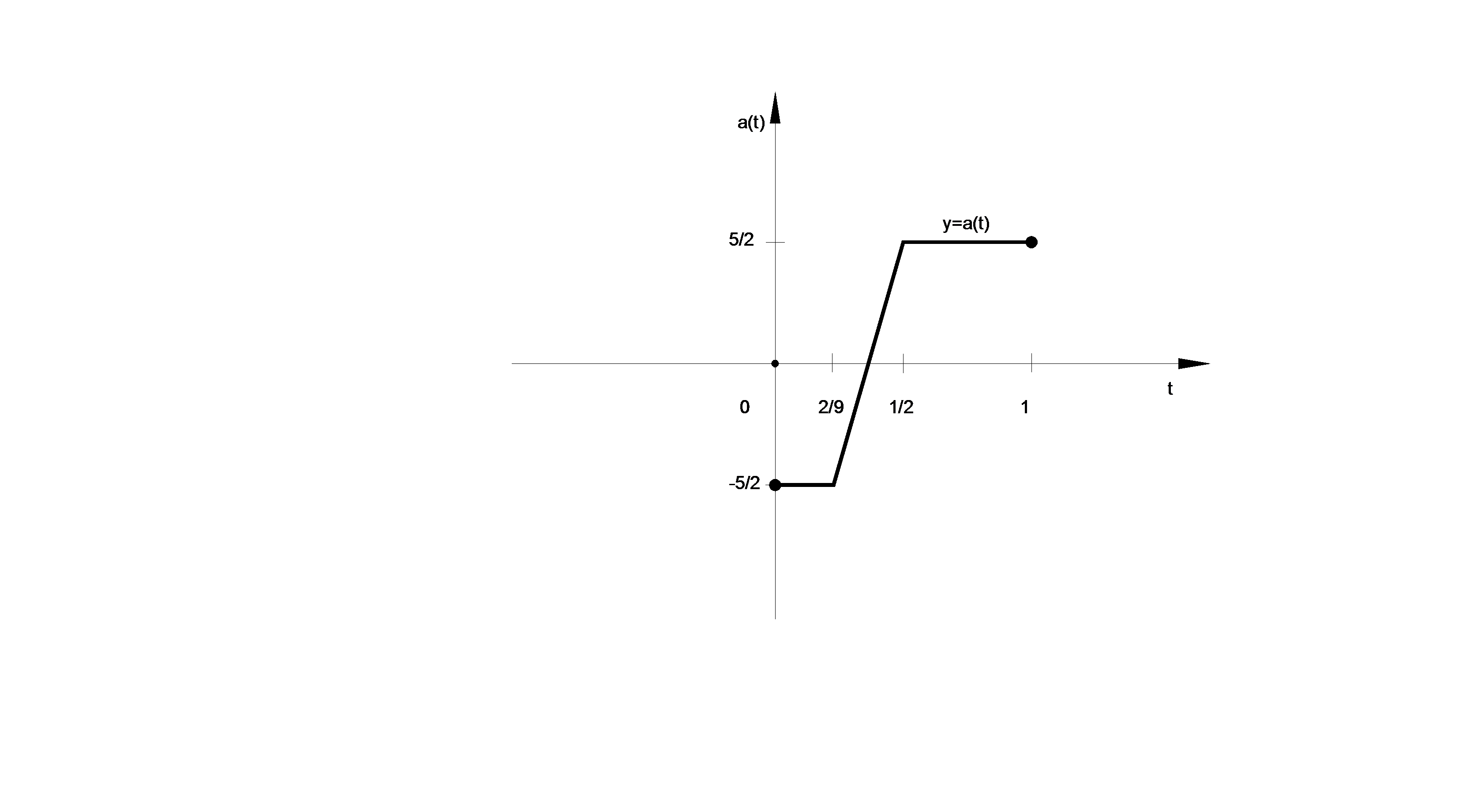
Рисунок 8 – График функции 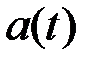
Тогда уравнение (7) имеет ненулевое решение (например, изображенное графически на рисунке). Значит,  . Рассуждая аналогично при
. Рассуждая аналогично при  , получим, что
, получим, что  .
.
Если  , то
, то  должно быть равно нулю всюду, за исключением одной точки (в которой
должно быть равно нулю всюду, за исключением одной точки (в которой  ). По непрерывности
). По непрерывности  всюду на отрезке
всюду на отрезке 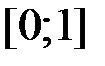 . Значит, точки интервала
. Значит, точки интервала  не принадлежат точечному спектру. Итак,
не принадлежат точечному спектру. Итак, 
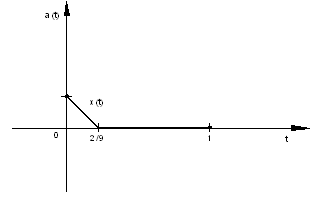
Рисунок 9 – График ненулевого решения уравнения (7)
Рассмотрим теперь уравнение (где  )
)
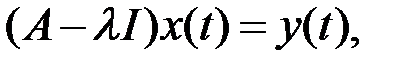
то есть
 . (8)
. (8)
Если  , то уравнение (8) имеет для любого у из
, то уравнение (8) имеет для любого у из  единственное непрерывное решение
единственное непрерывное решение
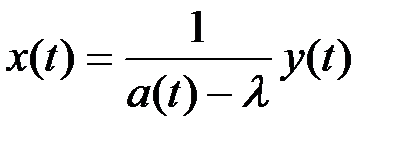 .
.
Значит, значения  , не принадлежащие отрезку
, не принадлежащие отрезку  , являются регулярными.
, являются регулярными.
Рассмотрим число  . Тогда существует
. Тогда существует  , такое, что
, такое, что  , и уравнение (8) разрешимо не для любого
, и уравнение (8) разрешимо не для любого  (почему?). Значит,
(почему?). Значит,  .
.
Покажем, что все  принадлежат остаточному спектру. По определению образа оператора,
принадлежат остаточному спектру. По определению образа оператора,
 .
.
Из того, что для любого  существует
существует  такое, что
такое, что  , следует, что при этих
, следует, что при этих  для любой функции
для любой функции  выполняется условие
выполняется условие  1):
1):  . Поэтому точка 1 не является точкой прикосновения для
. Поэтому точка 1 не является точкой прикосновения для  , а стало быть,
, а стало быть,  . Значит,
. Значит,  , а непрерывный спектр оператора А − пустое множество. Итак,
, а непрерывный спектр оператора А − пустое множество. Итак, 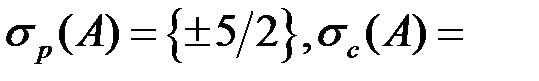 Ø
Ø  .
.
4. Найти спектр оператора  ,
,  .
.
Пример 1. 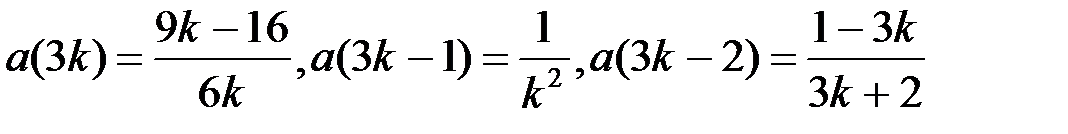 .
.
Решение. Данный оператор имеет вид
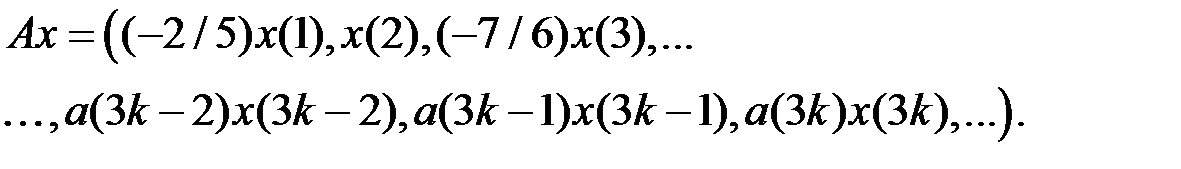
Рассмотрим уравнение  . Оно равносильно бесконечной системе уравнений
. Оно равносильно бесконечной системе уравнений
 .
.
Если  , то эта система имеет ненулевое решение (например, вида en). При других
, то эта система имеет ненулевое решение (например, вида en). При других  система имеет только нулевое решение. Таким образом,
система имеет только нулевое решение. Таким образом, 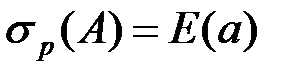 . Так как спектр − замкнутое множество, то он содержит свои предельные точки, в данном случае 3/2; 0; -1. Значит, он содержит и замыкание
. Так как спектр − замкнутое множество, то он содержит свои предельные точки, в данном случае 3/2; 0; -1. Значит, он содержит и замыкание  =
=  .
.
Предположим теперь, что  , и рассмотрим уравнение
, и рассмотрим уравнение
 ,
,
т. е. бесконечную систему линейных уравнений ( )
)
 . (9)
. (9)
Ее решение дается равенствами ( )
)
 .
.
Выясним, принадлежит ли найденная последовательность 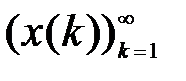 пространству
пространству  . Так как
. Так как  , то
, то 
 . Тогда
. Тогда
 ,
,
так как  . Следовательно, если
. Следовательно, если  , то уравнение (9) однозначно разрешимо в
, то уравнение (9) однозначно разрешимо в  при любом
при любом  . Значит, в этом случае
. Значит, в этом случае  . Итак,
. Итак,
 .
.
5. Выяснить, может ли следующее множество  быть спектром некоторого линейного ограниченного оператора. В случае положительного ответа привести пример такого оператора.
быть спектром некоторого линейного ограниченного оператора. В случае положительного ответа привести пример такого оператора.


 .
.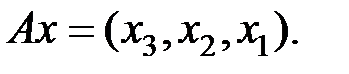
 , при которых уравнение
, при которых уравнение  имеет ненулевые решения. Но это уравнение равносильно следующей однородной системе линейных уравнений:
имеет ненулевые решения. Но это уравнение равносильно следующей однородной системе линейных уравнений: ,
, . По следствию из правила Крамера эта система имеет ненулевое решение тогда и только тогда, когда ее главный определитель равен нулю. Решая уравнение
. По следствию из правила Крамера эта система имеет ненулевое решение тогда и только тогда, когда ее главный определитель равен нулю. Решая уравнение  , находим, что
, находим, что 
 .
. .
.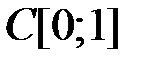
 , (1)
, (1) (2)
(2) , при которых это уравнение имеет ненулевое решение. Но из (2) следует, что
, при которых это уравнение имеет ненулевое решение. Но из (2) следует, что  при
при  , а тогда по непрерывности
, а тогда по непрерывности 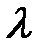 . Таким образом,
. Таким образом,  Ø.
Ø. )
) , (3)
, (3) . (4)
. (4) состоит из тех значений
состоит из тех значений  , при которых оператор
, при которых оператор  обратим, т. е. при таких значениях
обратим, т. е. при таких значениях  , то уравнение (4) однозначно разрешимо относительно
, то уравнение (4) однозначно разрешимо относительно 
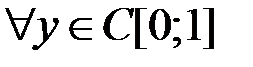 , а именно,
, а именно,  . В этом случае
. В этом случае  .
. , то уравнение (4) разрешимо в пространстве
, то уравнение (4) разрешимо в пространстве  (например, оно не имеет решения при
(например, оно не имеет решения при  , так как из равенства (4) следует, что
, так как из равенства (4) следует, что 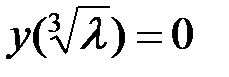 ). В этом случае
). В этом случае  .
.
 ,
,  .
. .
. , т. е.
, т. е. . (5)
. (5)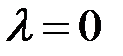 , то это уравнение имеет ненулевое решение (подходит любая непрерывная функция, для которой
, то это уравнение имеет ненулевое решение (подходит любая непрерывная функция, для которой  , например, функция
, например, функция  ). Значит,
). Значит, 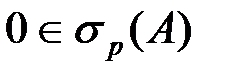 .
. , то, разделив на
, то, разделив на  ,из уравнения (5) выводим, что его решение должно иметь вид
,из уравнения (5) выводим, что его решение должно иметь вид  (k и b – неопределенные коэффициенты). Тогда
(k и b – неопределенные коэффициенты). Тогда  .
. , откуда
, откуда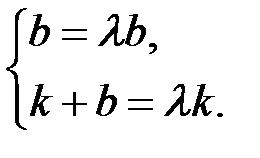
 или
или  . В случае
. В случае  система имеет ненулевое решение (например
система имеет ненулевое решение (например  ). А если
). А если  , то система, как легко проверить, имеет только нулевое решение. Итак, уравнение (5) имеет ненулевое решение лишь при
, то система, как легко проверить, имеет только нулевое решение. Итак, уравнение (5) имеет ненулевое решение лишь при 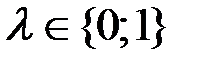 . Значит,
. Значит,  .
. ,
, , (6)
, (6) . Из (6) следует, что
. Из (6) следует, что .
. , получим
, получим  . Полагая в (6)
. Полагая в (6)  , находим, что
, находим, что .
. , то решение уравнения (6) имеет вид
, то решение уравнения (6) имеет вид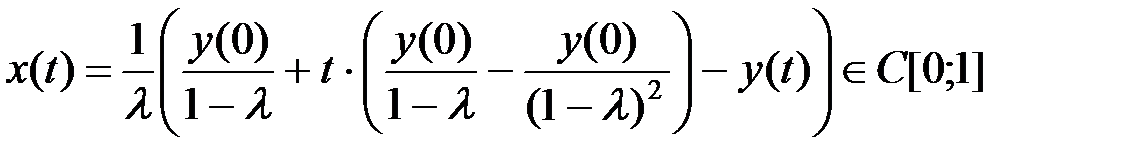 .
. уравнение (6) однозначно разрешимо в
уравнение (6) однозначно разрешимо в  для любого у из
для любого у из 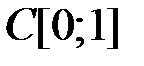 . Итак,
. Итак, 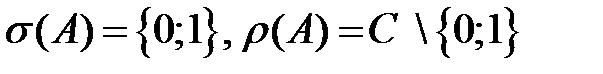 .
. , если
, если  .
. .
. метод интервалов, получим
метод интервалов, получим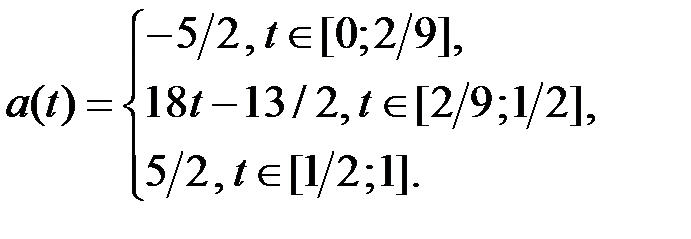
 (рисунок 8). Рассмотрим уравнение
(рисунок 8). Рассмотрим уравнение  , то есть
, то есть  , или
, или . (7)
. (7) , то уравнение (7) имеет только нулевое решение. Если
, то уравнение (7) имеет только нулевое решение. Если  , то
, то 
 .
.
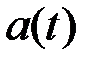
 . Рассуждая аналогично при
. Рассуждая аналогично при  , получим, что
, получим, что  .
. , то
, то  должно быть равно нулю всюду, за исключением одной точки (в которой
должно быть равно нулю всюду, за исключением одной точки (в которой  ). По непрерывности
). По непрерывности  всюду на отрезке
всюду на отрезке 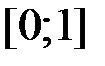 . Значит, точки интервала
. Значит, точки интервала  не принадлежат точечному спектру. Итак,
не принадлежат точечному спектру. Итак, 

 )
)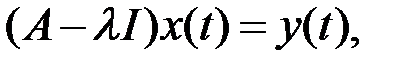
 . (8)
. (8) , то уравнение (8) имеет для любого у из
, то уравнение (8) имеет для любого у из  единственное непрерывное решение
единственное непрерывное решение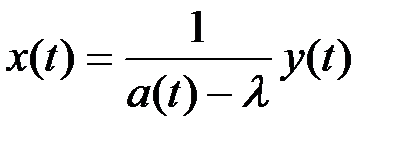 .
. , не принадлежащие отрезку
, не принадлежащие отрезку  , такое, что
, такое, что  , и уравнение (8) разрешимо не для любого
, и уравнение (8) разрешимо не для любого  (почему?). Значит,
(почему?). Значит,  .
. .
. , следует, что при этих
, следует, что при этих  для любой функции
для любой функции  выполняется условие
выполняется условие  1):
1):  . Поэтому точка 1 не является точкой прикосновения для
. Поэтому точка 1 не является точкой прикосновения для  , а стало быть,
, а стало быть,  . Значит,
. Значит,  , а непрерывный спектр оператора А − пустое множество. Итак,
, а непрерывный спектр оператора А − пустое множество. Итак, 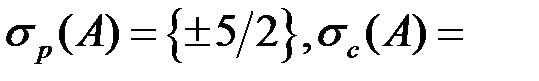 Ø
Ø  .
. ,
,  .
.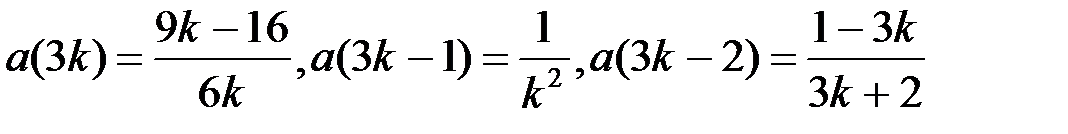 .
.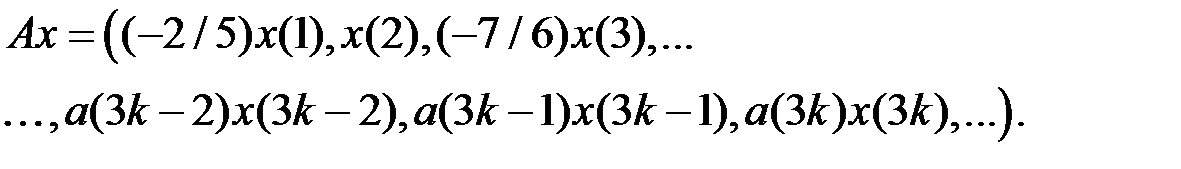
 . Оно равносильно бесконечной системе уравнений
. Оно равносильно бесконечной системе уравнений .
. , то эта система имеет ненулевое решение (например, вида en). При других
, то эта система имеет ненулевое решение (например, вида en). При других  система имеет только нулевое решение. Таким образом,
система имеет только нулевое решение. Таким образом, 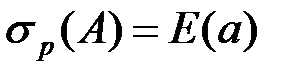 . Так как спектр − замкнутое множество, то он содержит свои предельные точки, в данном случае 3/2; 0; -1. Значит, он содержит и замыкание
. Так как спектр − замкнутое множество, то он содержит свои предельные точки, в данном случае 3/2; 0; -1. Значит, он содержит и замыкание  =
=  .
. , и рассмотрим уравнение
, и рассмотрим уравнение ,
, )
) . (9)
. (9) .
.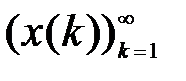 пространству
пространству  . Так как
. Так как  , то
, то 
 . Тогда
. Тогда ,
, . Следовательно, если
. Следовательно, если  , то уравнение (9) однозначно разрешимо в
, то уравнение (9) однозначно разрешимо в  . Значит, в этом случае
. Значит, в этом случае  . Итак,
. Итак, .
. быть спектром некоторого линейного ограниченного оператора. В случае положительного ответа привести пример такого оператора.
быть спектром некоторого линейного ограниченного оператора. В случае положительного ответа привести пример такого оператора.


